timnswede
- 100
- 0
Problem is in the picture below.
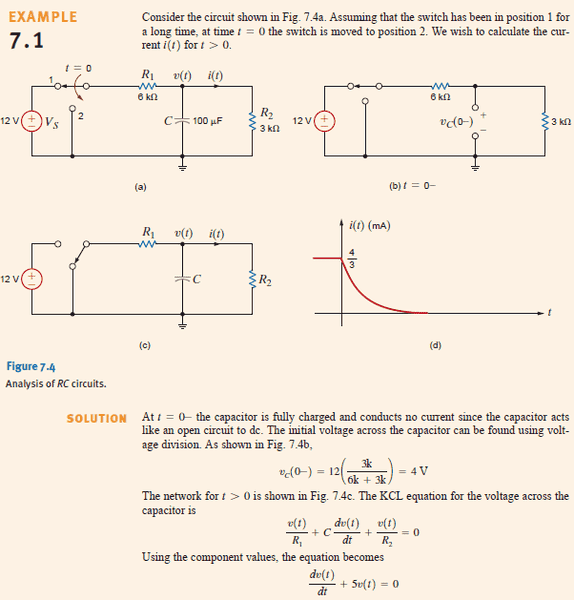
The problem is already solved, but I am confused as to why C(dv/dt) is positive and not negative, since the current is coming out of the capacitor and towards the point v(t), which is not away from v(t) like the solution shows. But if I solve the problem with the negative sign there I get an infinite voltage which obviously makes no sense. Can someone explain why we assume it's going away, unlike what would be done if it was a given current source?
The problem is already solved, but I am confused as to why C(dv/dt) is positive and not negative, since the current is coming out of the capacitor and towards the point v(t), which is not away from v(t) like the solution shows. But if I solve the problem with the negative sign there I get an infinite voltage which obviously makes no sense. Can someone explain why we assume it's going away, unlike what would be done if it was a given current source?