Confused - Materials question regarding c/a ratio

[Rajveer97]

Hi everyone, first time poster here, I'm studying for a Materials exam, one of my weakest subjects and this question is causing me a lot of pain:

Beryllium (Be) is a HCP metal with an atomic weight of 9 g mol-1 , an atomic radius of 0.112nm and a density of 1850 kg m-3 . Calculate its c/a ratio given that Avogadro’s number is 6.02×1023 mole-1 .

Here's the working after some basic steps

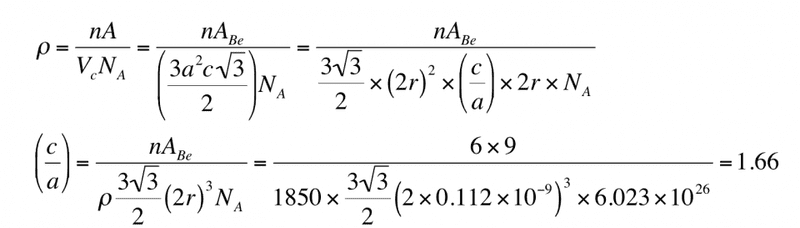
The thing that I don't understand is how this

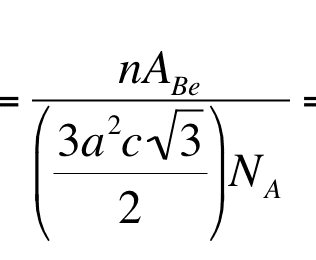
becomes this

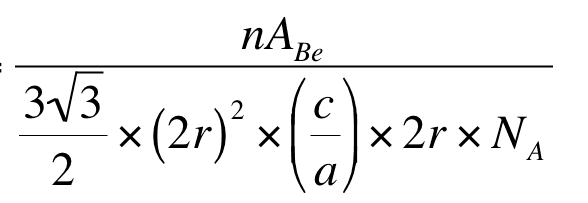
How are there two 2r there now? Where is the (c/a) coming from? I just can think through that, how does one get to that? Any help would be greatly appreciated I'm really stuck!
Thanks

 

[Irene Kaminkowa]

Hi,
as far as I see
$$a^2c=a^3\cdot \frac{c}{a}=\left ( 2r \right )^3\cdot \frac{c}{a}$$

 

[Rajveer97]

Hi,
as far as I see
$$a^2c=a^3\cdot \frac{c}{a}=\left ( 2r \right )^3\cdot \frac{c}{a}$$

That seems to be the only possible answer, thanks! :)