Confusion about induction in conductors

[timetraveller123]

Homework Statement

Homework Equations

The Attempt at a Solution

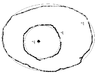
a) charge induced is
$\frac{-q_i}{4 \pi r_i^2} = \sigma_i$
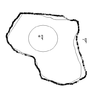
$\frac{q_a + q_b}{4 \pi R^2} = \sigma_R$

b) field outside is $\frac{k (q_a + q_b)}{r^2}$

c)i naively applied gauss law to get field within each cavity as

$\frac{k q_i}{r_i^2}$

d) i was assuming the only field in the cavity is due to charge itself only and due to induced charge on the inner surface hence force = 0 which is correct

but part e confuses me

e)
the provided answer

how could $sigma_r$ change and still have the $\sigma_a$ and $sigma_b$ constant while the conductor is neutral

furthermore this another text states
"The field inside the cavity depends only on the charge q and on the charge that gets induced on the inner surface of the cavity."
how could the induced surface charges affect the field inside if they are not included in the Gaussian surface

 

[kuruman]

In part (e) bringing the third charge near the conductor pushes charges around on the surface thus changing the distribution of surface charges but not the total charge on the surface. Because the electric field is zero inside the conductor and remains zero, what goes on inside does not affect what's outside and vice-versa.

Charges communicate with other charges via electric fields. Since there is no electric field inside the conductor, that line of communication is severed. The induced surface charges do not affect the field inside for that reason. I think you misunderstood what the textbook meant, namely that the field inside the cavity depends only on the charges that are placed inside the cavity and the surface distribution on the inside surface of the cavity. If you place a charge +q inside a cavity in a conductor, the total induced charge on the inner surface will be -q regardless of the shape of the cavity. However, the electric field inside the cavity will depend on the shape. A spherical cavity will have a different field inside it from a cube-shaped cavity. Don't forget that electric field lines have to be perpendicular to the conducting surface.

 

[timetraveller123]

so is this what you are saying
when there was no third charge, the $\sigma_R$ was evenly distributed on the surface of the conductor but when the third charge was placed $\sigma_R$ just redistributed itself and in sense "the magnitude of "$\sigma_R$ did not change

If you place a charge +q inside a cavity in a conductor, the total induced charge on the inner surface will be -q regardless of the shape of the cavity.

this i understand is to make the field in the conductor zero

namely that the field inside the cavity depends only on the charges that are placed inside the cavity and the surface distribution on the inside surface of the cavity.

this is what i don't understand

now is the -q charge referred to as the surface charge induced on inside cavity i don't see how could the -q surface charge affect the field inside the cavity

if we draw a gaussian surface inside the cavity enclosing only the +q charge then the field inside is only due to +q charge and that was the answer to part c which was correct
so what do you mean by

However, the electric field inside the cavity will depend on the shape. A spherical cavity will have a different field inside it from a cube-shaped cavity.

i hope you can understand what is tripping me up thanksedit :
upon more careful thinking i am realizing that the E.da in gauss law is the net flux and and to which the surface charge does not contribute but that does not mean the field due to the surface charge is not there

 

[kuruman]

o is this what you are saying
when there was no third charge, the σR\sigma_R was evenly distributed on the surface of the conductor but when the third charge was placed σR\sigma_R just redistributed itself and in sense "the magnitude of "σR\sigma_R did not change

Yes, that's what I'm saying.

his i understand is to make the field in the conductor zero

Good.

if we draw a gaussian surface inside the cavity enclosing only the +q charge then the field inside is only due to +q charge and that was the answer to part c which was correct

Yes, I agree that part (c) is correct. However, I suspect that you think that the electric field inside the cavity will be $kq_i/r_i^2$ no matter where the charge is placed or what the shape of the cavity is. This result is correct only in the highly symmetrical case of a spherical cavity with the charge at its center. That's what I wanted to clarify.

 

[timetraveller123]

um i just edited it would you mind looking at it

 

[timetraveller123]

i am thinking that my problem is just with what's going on in the cavity so let me just focus on the cavity say we have arbitrarily shaped cavity containing a charge q then on the outside there is -q induced charge

what i am saying is that where the geometry permits isn't it possible to construct a sperical gaussian surface with the charge in the centre to conslude that $\vec{E} = \frac{k q}{ r^2}$ and in other parts of the cavity we will have to take into account the dot product and the surface charge is that what you are saying

 

[kuruman]

upon more careful thinking i am realizing that the E.da in gauss law is the net flux and and to which the surface charge does not contribute but that does not mean the field due to the surface charge is not there

Yes the surface charge is there and affects the field. Gauss's Law is always valid. What you cannot always do is say that
$$\int{\vec{E}\cdot \hat{n}dA} =E\int{dA}$$
This happens when the electric field is perpendicular to the Gaussian surface and constant everywhere on the Gaussian surface.

 

[timetraveller123]

yes now i get it one last question in the case of electrostatic shielding we know it is something like this (although the field lines bend)

where black is negative charge and pink is positive charge
but what if a external electric field pierces the conductor radially at all parts like this

at equal magnitude at all point then how can the charges redistribute themselves i don't see any possible way thanks

 

[kuruman]

Suppose you draw a Gaussian surface just above the surface of the conductor. You have negative electric flux through that surface. What is the inescapable conclusion according to Gauss's Law?

 

[timetraveller123]

oh my i completely forgot it is a negative charge wow that is very elegant indeed
but is there any way to direct the electric field radially towards a neutral conductor by external means ?
would that just crush the conductor?(due to electrostatic pressure)

 

[kuruman]

but is there any way to direct the electric field radially towards a neutral conductor by external means ?

You can place the neutral conducting sphere concentric with a conducting shell. You connect the outer shell to the positive terminal of a dc power supply and the sphere to the negative terminal. (I am describing a charged spherical capacitor.) In the region between the shell and the sphere you will get radial electric field lines as you imagined. Will the inner sphere be crushed if you crank up the power supply? Don't forget that if the outer shell is positively charged and the inner sphere has uniformly negative charges on its surface moved there by the power supply. There will be attraction between the positive outer charges and the negative inner charges so that the inner sphere will tend to explode rather than be crushed. Can you have the radially inward electric field without a negative charge in the center? The answer is no because that would violate Gauss's Law as indicated in post #9.

 

[timetraveller123]

sorry for the late reply i was thinking what would happen
if we were to plop down a ring of positive charge around the metal sphere the field only cancels out in the centre so there might still be some radial field at points off the centre then what happens in that situation will the metal sphere be repelled by it somehow

 

[kuruman]

... will the metal sphere be repelled by it somehow

Keep in mind that in a conductor some of the electrons are free to move around in response to electric fields. They will move and keep on moving until the electric field inside the conductor becomes zero. This happens very fast. As a result, any electric field lines on the outside that impinge on the conductor, must stop at the surface. If the lines are generated on the outside by positive charges, they start there and end on the conductor's surface. If the outside charges are negative, electric field lines start on the surface of the conductor and end at those negative charges. This is another way of saying that the induced charges on the surface of the inductor have polarity that is always opposite to the outside charges as the free electrons in the conductor are attracted by negative external charges and repelled by positive external charges. Even if the conductor is neutral, there will be separation of charges inside it and you will have opposite charges on the surface in closer proximity than the charges of the same polarity. This makes the net force between the external charges and the conductor always attractive.

 

[timetraveller123]

ok now i see it but one last question

say considering the same positive ring of charge
inside the ring the field points radially inwards again except for at the origin where it is zero but inside the ring there is no charge but any Gaussian envelope will net negative flux what is solution to this do i have to consider it in three dimensions ?

 

[kuruman]

... inside the ring the field points radially inwards again except for at the origin where it is zero.

Not really. See simulation of electric field lines due to a ring of charge in Figure 29 here.
http://web.mit.edu/8.02t/www/802TEAL3D/visualizations/guidedtour/Tour.htm#_Toc27302329

... do i have to consider it in three dimensions ?

Of course. How else are you going to enclose a volume with a Gaussian surface?

 

[timetraveller123]

so while there is "negative divergence" in the xy plane but in total when considering the three dimension there is also some positive divergence hence exactly canceling out?
nice link by the way thanks!

 

[kuruman]

so while there is "negative divergence" in the xy plane but in total when considering the three dimension there is also some positive divergence hence exactly canceling out?

Exactly.

 

[timetraveller123]

thank you very much for your help ! :)