- #1
sss1
- 50
- 2
- Homework Statement
- In the picture
- Relevant Equations
- Gauss's law
Is this a good response?
The lift is a conductor, therefore electrons can move freely. The charges on a conductor reside on the outer surface as they like to be as far from each other as they possibly can be due to the repulsive coulomb force. There is no charge between the inner and the outer surface of the box, the charge distribution on the outside of the box will not be uniform since its not spherical in shape. There will be more charges at the corners of the box. Using Gauss's law, drawing a rectangular Gaussian surface with width greater than the inner surface but smaller than the outer surface, the net enclosed charge inside the lift is 0 whether or not if there is charge on the student; the electrons inside the conductor will rearrange themselves to cancel out the electric field carried by the charge. Hence there is no electric field inside the lift, and so the radio does not work as it requires external electromagnetic signals. Outside the box, since negatively charged electrons reside on the surface, the electric field will terminate at the surface of the box.
I'm thinking of something like this for the diagram?
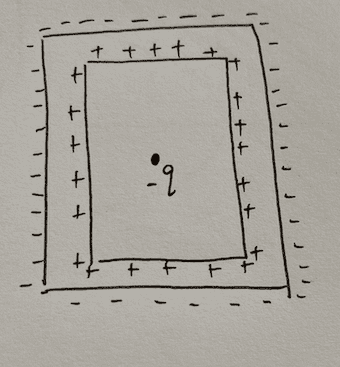
With regards to the charge distribution on the inner surface, doesn't that depend on whether or not the student has any charge? If the student carries some negative charge then there will be an induced positive charge around the inner surface; and there will be negative charges on the outer surface. Whereas if the student carries positive charge then there will be induced negative charge; and there will be positive charges on the outer surface.

The lift is a conductor, therefore electrons can move freely. The charges on a conductor reside on the outer surface as they like to be as far from each other as they possibly can be due to the repulsive coulomb force. There is no charge between the inner and the outer surface of the box, the charge distribution on the outside of the box will not be uniform since its not spherical in shape. There will be more charges at the corners of the box. Using Gauss's law, drawing a rectangular Gaussian surface with width greater than the inner surface but smaller than the outer surface, the net enclosed charge inside the lift is 0 whether or not if there is charge on the student; the electrons inside the conductor will rearrange themselves to cancel out the electric field carried by the charge. Hence there is no electric field inside the lift, and so the radio does not work as it requires external electromagnetic signals. Outside the box, since negatively charged electrons reside on the surface, the electric field will terminate at the surface of the box.
I'm thinking of something like this for the diagram?
With regards to the charge distribution on the inner surface, doesn't that depend on whether or not the student has any charge? If the student carries some negative charge then there will be an induced positive charge around the inner surface; and there will be negative charges on the outer surface. Whereas if the student carries positive charge then there will be induced negative charge; and there will be positive charges on the outer surface.