Confusion in Maxwell's derivation of Ampere's Force Law - II

[faheemahmed6000]

I am reading Maxwell's "a treatise on electricity and magnetism, Volume 2, page 156" about "Ampere's Force Law". I have some confusion in the following pages:

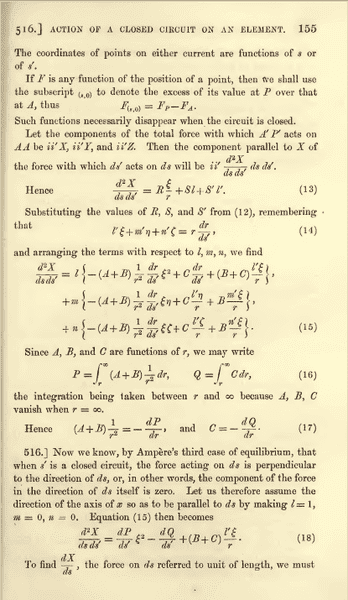
My question is of two parts:
1.Equation 20, i.e. $P=\dfrac{B+C}{2r}$ is the outcome of special case (i.e. l=1, m=0, n=0)

But in Page 156, Article 517, Maxwell says: "We can now eliminate P, and find the general value of $\dfrac{dX}{ds}$" and uses this formula (i.e. $P=\dfrac{B+C}{2r}$) in the general case.

However in the general case, where 0 < l, m, n < 1, and hence
$\dfrac{d^{2}X}{dsds'}=l\left( \frac{dP}{ds'}\xi^{2}-\dfrac{dQ}{ds'}+(B+C)\dfrac{l'\xi}{r}\right) +m(...)+n(...)\neq0$
(since direction of X is not in the direction of ds)

therefore,
$\dfrac{dX}{ds}=l\left[ (P\xi^{2}-Q)_{(s',0)}-\int\limits_0^s' (2Pr-B-C)\dfrac{l'\xi}{r}ds'\right] +m\int\limits_0^s'(...)ds'+n\int\limits_0^s'(...)ds'$
Now in this general case, how can we get $P=\dfrac{B+C}{2r}$.

If $P\neq\dfrac{B+C}{2r}$ in general case, what does Maxwell mean by "We can now eliminate P, and find the general value of $\dfrac{dX}{ds}$"
2. How can one get equation 21 from equation 15. Please give a lengthy derivation.

 

[vanhees71]

Well, it's a pity that you get no answers. My problem is that I have not the time to decipher Maxwell's ancient notation to make sense of it. Perhaps, it helps, if you "translate" the argument in modern standard notation of vector calculus?

 

[faheemahmed6000]

Up to here (page 156), there is no dot or cross product and the language and notation (except a few) are common. I had nothing to 'decipher' up to page 156 (except to solve a few maths). What I only don't understand (up to page 156) is the generalisation of $P=\dfrac{B+C}{2r}$. Can you please go through the pages and explain why $P=\dfrac{B+C}{2r}$ is generalised for all values of $l, m, n$ as well as for open circuits while it is derived from special case $(l=1, m=0, n=0)$? There is nothing hard to decipher here. I am reading this old book because this is only where I find a historic derivation of Ampere's Force Law. Any help would be appreciated.

 

[vanhees71]

Well, I've no clue what all the symbols mean and thus have even less a clue what Maxwell is doing there :-(. It's very hard for me to follow 19th century literature before the invention of modern vector notation (which is, as far as I know, due to the successors of Maxwell like Heaviside and Poynting in applying his theory to the upcoming engineering problems related to telegraphs, sea cables, etc.). Even the electromagnetic part of Einstein's famous paper of 1905 about special relativity is very hard to read, because he writes out everything in terms of components of the fields. If you "translate" it to modern notation, it's pretty quickly obvious, what he is doing!

 

[faheemahmed6000]

How do I translate it to vector notation

 

[facenian]

I believe that what you are doing belongs to the history and philosphy of science. If you want lo learn the subject I suggest you do it in the modern way.It is eassier in that way