Pushing a rod in a magnetic field

[Juanda]

TL;DR Summary

I would like to better understand the interconnection between induced current, circuits, and Newton's laws.

I will present the case as an exercise because I believe it will be easier to understand that way. I didn't know if I should post it under the mechanics or electromagnetism sections because I am actually trying to link both. Since it feels like a fairly simple problem, I considered the Classical Physics area could be fine.


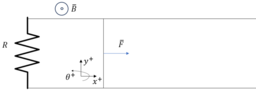
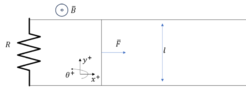
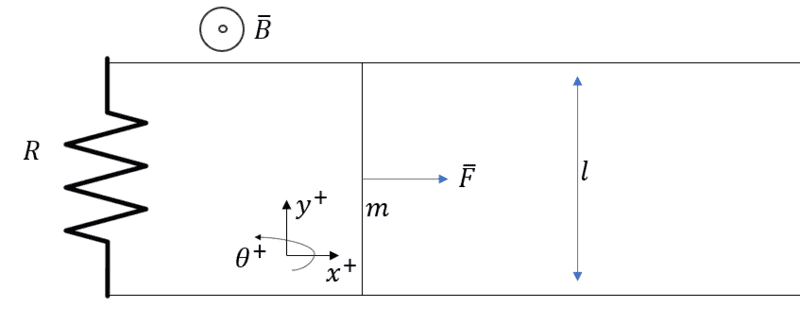
There is a rod of mass $m$ that closes a circuit. The rod can move as shown in the image.
The circuit contains a constant resistance $R$.
The resistance of the conductor and the rod is negligible.
There is a magnetic field $B$ present that can be considered constant, uniform, and perpendicular to the circuit.
A constant force is applied to the rod.

1. Describe the movement of the rod.
2. Describe the energy consumption over time.

Using Faraday's law I can find what is the energy consumption on $R$ because of the voltage generated at a given velocity. However, I cannot link that to Newton's laws so I cannot really know how the velocity of the rod changes.
Here is my attempt so far.
$$V=-\frac{d\Phi}{dt}=-\frac{d}{dt}\int \bar{B}d\bar{S}$$
The normal vector to the changing surface is parallel to the magnetic field so the dot product is simplified. This is:
$$\bar{B}d\bar{S}=BdS$$
The change in the surface $dS$ can be described as:
$$dS=ldx$$
From the definition of velocity, $dx$ can be expressed as:
$$\frac{dx}{dt}=v \rightarrow dx=vdt \rightarrow dS=lvdt$$
Going back to the expression of voltage due to the change in magnetic flux on an area, the equation cancels the integral and the derivative over time:
$$V=-\frac{d\Phi}{dt}=-\frac{d}{dt}\int BdS=-\frac{d}{dt}\int Blvdt=-Blv$$
If that voltage is connected to $R$ as initially described, then there will be a current induced in the circuit and power dissipation in the resistance.
$$P=\frac{V^2}{R} = \frac{(-Blv)^2}{R}$$
Given enough time, the problem will be almost stationary. I could use energy conservation to estimate the magnetic "friction" force on the rod.
$$P=\frac{V^2}{R}=Fv \rightarrow F = \frac{B^2l^2v}{R}$$

What is the actual expression of the "magnetic friction"? What I obtained is assuming a few things to get there.
What is the coupled system of equations that links the generation of power due to induction, the circuit, and Newton's laws?

Thanks in advance.

 

[kuruman]

The connection to Newton's second law can be obtained by drawing a free body of the rod. You have two external forces acting on the the rod, the constant applied force $\mathbf{F}$ and the magnetic force $\mathbf{F}_M=I_{ind}~\mathbf{L}\times\mathbf{B}$ due to the induced current according to Faraday's law. Note the magnetic force opposes the motion.

The form that you got for the "magnetic friction is correct. If you are not satisfied with your derivation, here is mine. No surface integral is needed because the field is uniform. By Faraday' law
$$\text{emf}=-\frac{d\phi}{dt}=-B\frac{dA}{dt}=-Blv$$ The induced current in the loop of resistance $R$ is $$I_{ind}=\frac{emf}{R}=-\frac{Blv}{R}$$and the magnetic force is $$F=-\frac{B^2l^2}{R}v.$$Newton's law is $$m\frac{dv}{dt}=F-\frac{B^2l^2}{R}v.$$This is an ordinary first order differential equation that you can solve in any number of ways. You can see that the rod has a terminal velocity which you can find by setting the acceleration equal to zero. $$0=F-\frac{B^2l^2}{R}v_{\text{ter}}\implies v_{\text{ter}}=\frac{FR}{B^2l^2}.$$

 

[Juanda]

The connection to Newton's second law can be obtained by drawing a free body of the rod. You have two external forces acting on the the rod, the constant applied force $\mathbf{F}$ and the magnetic force $\mathbf{F}_M=I_{ind}~\mathbf{L}\times\mathbf{B}$ due to the induced current according to Faraday's law. Note the magnetic force opposes the motion.

Thank you. That is what I was missing. I knew about $\overrightarrow{F}=q(\overrightarrow{E}+\overrightarrow{v} \times \overrightarrow{B})$ and similar expressions but it's been so long without using it that I didn't think about the connection.

I have a few more questions related to this post. For the moment they are:

1. Let's remove the circuit and consider the rod has some resistance. If I move the rod in the same way, is it OK to treat it as the same circuit but with a capacitor in line? With the information you provided, I should even be able to get the equations that describe the situation.
2. If instead of moving the rod horizontally, I rotated it, the relation with $v$ would be a little more complex but the whole thing would still be the same. Right?
3. If instead of rotating a rod, I rotated a solid disk, I don't really know how to fit the equations shown so far to that situation. Would such a configuration be an effective Eddy Current Damper?

I'm wondering if it is better to post them here or to make a separate post. I will do as you prefer.

 

[kuruman]

It's OK to post here because your questions are related.

Read about your first two questions motional emf here.
For the third question read about the homopolar generator here. Yes, it could also be considered an eddy current damper.

Come back if you have more questions.

 

[Juanda]

Those two links are very accurate. The one about the homopolar generator turned out to be quite a rabbit hole with Faraday's Paradox so I'll try to advance little by little.

I'd like to continue the case for the isolated rod moving through a magnetic field which I think is the simplest continuation and I couldn't find what I have in mind in the links you shared.
The rod has its own resistance. To calculate it is necessary to add some data. Let's say it's got a constant circular section $A$ and a length $l$. The resistivity will be considered independent of temperature and is $\rho$. Therefore, the electrical resistance of the rod is:
$$R=\frac{\rho l}{A}$$
As mentioned in post 3, if the rod is not connected to anything, I think it can be considered a capacitor because all the free electrons will bunch up on one side of the rod. Or maybe that's not a capacitor but an electrical dipole. I will assume it is a capacitor but I don't know how to calculate the capacitance of such a rod. The closest I could find is the capacitance of a hollow cylinder but that is not the same scenario. For now, let's say the capacitance $C$ is known although I'd like to know if calculating it is achievable.

Assuming it is an ideal world, would I need an additional pair of forces to keep the rod straight? In other words, would the magnetic field $B$ apply a torque on the rod because of the charge distribution?
To simplify it, I will assume both ends are fixed on rollers so the rod cannot turn in $\theta$ but can move horizontally in $x$.
Would this be the equivalent electrical circuit?

The coupled system of differential equations to describe the problem would be the one that solves the circuit and Newton's.
$$V_{ac}=V_{ba}+V_{cb} \rightarrow -Bl \dot x = \frac{1}{C}\int idt+iR$$
$$F-F_{ind}=m\ddot x \rightarrow F-ilB=m\ddot x$$

Summary of my questions regarding this post:

1. Is it OK to assume the rod is behaving like a capacitor as shown or should I consider something else because it would look like an electric dipole?
2. If it is OK to think of it as a capacitor, how could I find the $C$?
3. Is the magnetic field $B$ going to cause a torque on the rod I'd need to counteract with an external torque if I want it to move only horizontally?
4. Is there any additional error in the reasoning that is not included in the previous questions?

Thanks in advance.

 

[Juanda]

Can I post this second version of the problem in the Electromagnetism section?
Maybe there is someone there who can provide more feedback about it. I want to work my way up towards Eddy Current Dampers and the Homopolar Generator / Faraday Motor and I feel these preliminary questions are necessary to build a proper foundation.

By the way, I mentioned the pair of forces necessary to keep the rod straight during the process. I wasn't certain before but they must exist. For now, let's assume the rod is mounted on rollers that keep it oriented as shown to simplify the problem.

View attachment 341195

Assuming it is an ideal world, would I need an additional pair of forces to keep the rod straight? In other words, would the magnetic field $B$ apply a torque on the rod because of the charge distribution?
To simplify it, I will assume both ends are fixed on rollers so the rod cannot turn in $\theta$ but can move horizontally in $x$.

 

[kuruman]

Can I post this second version of the problem in the Electromagnetism section?

Sure, why not?

As far as the rod moving in a uniform magnetic field at constant velocity is concerned, I think you need a conceptual foundation in order to think about it correctly. That is the Lorentz transformation equations for electromagnetism. They predict that an observer moving with velocity $\mathbf{v}$ relative to a uniform magnetic field $\mathbf{B}$ will see in his rest frame a uniform electric field given by $~\mathbf{E}=\mathbf{v}\times \mathbf{B}~$ and no magnetic field.

So imagine yourself moving along the rod. You will see a conductor in an external electric field which, as far as you are concerned, will redistribute the charges inside the conductor as needed to have the conductor be an equipotential. This separation of charges is not like the separated charges in a capacitor primarily because there is a conducting path between them. In a capacitor there is a gap which the charges cannot cross.

Furthermore, a capacitor is formed when you have two physically separated electrically neutral conductors of arbitrary shape in close proximity with one another. If you take charge $+Q$ from one conductor and place it on the other, you will end up with the first conductor having net charge $-Q$, and the other conductor having charge $+Q$. The will be a potential difference $\Delta V$ between the conductors and the capacitance will be $C=Q/\Delta V.$ This is not what you have when a rod is moving in a uniform magnetic field.

There is no torque acting on the rod. Your picture in post #5 is incomplete. The rod is electrically neutral. If you have an accumulation of negative charges at one end, there must be a deficit of negative charges, i.e. an equal in magnitude accumulation of positive charges at the other end. However, these induced charges are not fixed where they are and do not form an electric dipole. If you tip the rod, they will redistribute themselves.

I would encourage you to investigate your interests on the web and post specific questions that may arise on separate threads.

 

[Juanda]

I tried reading related posts in the forum but I couldn't find what I was specifically looking for.Before I go to the Electromagnetism Section to post there I'd like to clarify a couple of things. I want to see where my reasoning fails if it is wrong in the first place.

• Torque on the rod due to the magnetic field.
  Yes, the picture is incomplete. I only drew the electrons bunching up in one end. Protons would be fixed in place which results in a negative pole on one side and a positive pole on the other. Now, according to the electromagnetic forces suffered by charged particle $\overrightarrow{F}=q(\overrightarrow{E}+\overrightarrow{v} \times \overrightarrow{B})$ the forces are:
  The top side with the negative charge accumulation will suffer a force going up. (Right-hand rule but the other way because of the negative charge)
  The bottom side with the positive charge accumulation will suffer a force going down. (Right-hand rule)
  You are right. There is no net torque on the rod. The forces that show up are those that cause the accumulation of charge in the first place. I was using the right-hand rule incorrectly and I wasn't getting equilibrium because a net torque appeared.
• Considering the rod as a capacitor.
  So typically a capacitor accumulates charge on each face and can be connected as shown:
  
  
  In that example, the voltage source could be a battery. Similarly, as with the rod, the electrons move around and cause a negative pole where they bunch up and a positive pole in the gaps they leave behind.
  In this case, however, I'm considering the voltage source to be the induced voltage. The electric field would sure not be as straightforward as in the parallel capacitor with big flat faces close to each other but I see enough resemblance to make me think it'd be valid to consider the rod as a capacitor too. Calculating the $C$ of such a capacitor is another issue I haven't tried to face yet as I mentioned in previous posts.
  
  
  
  So, why is it wrong to model the problem considering the rod a capacitor so the resulting circuit is as in post #5
  
  

• Would this be the equivalent electrical circuit?
  View attachment 341197
  
  The coupled system of differential equations to describe the problem would be the one that solves the circuit and Newton's.
  $$V_{ac}=V_{ba}+V_{cb} \rightarrow -Bl \dot x = \frac{1}{C}\int idt+iR$$
  $$F-F_{ind}=m\ddot x \rightarrow F-ilB=m\ddot x$$

  
  

 

[kuruman]

So, why is it wrong to model the problem considering the rod a capacitor so the resulting circuit is as in post #5

I already explained that to you in post #7

Furthermore, a capacitor is formed when you have two physically separated electrically neutral conductors of arbitrary shape in close proximity with one another. If you take charge $+Q$ from one conductor and place it on the other, you will end up with the first conductor having net charge $-Q$, and the other conductor having charge $+Q$. The will be a potential difference $\Delta V$ between the conductors and the capacitance will be $C=Q/\Delta V.$ This is not what you have when a rod is moving in a uniform magnetic field.

I will say the same thing with pictures.

Look at the picture below left. It shows your model of a charged capacitor. If I put a short with a switch (in red) and close switch S, the capacitor will discharge and a steady current will flow in the resistor.

Look at the picture below right. If I short the two ends and close the switch, I will have a rectangular loop moving in a uniform field with no change in magnetic flux. There will be no current.

 

[Juanda]

I will say the same thing with pictures.

Look at the picture below left. It shows your model of a charged capacitor. If I put a short with a switch (in red) and close switch S, the capacitor will discharge and a steady current will flow in the resistor.

Look at the picture below right. If I short the two ends and close the switch, I will have a rectangular loop moving in a uniform field with no change in magnetic flux. There will be no current.

View attachment 341898View attachment 341897

The fact that there is no current in the second circuit when the switch is flipped made a little click in my head.
I still don't fully get why I cannot consider it a capacitor when the switch is open but I think I'm getting there.
Thanks.

 

[kuruman]

I still don't fully get why I cannot consider it a capacitor when the switch is open but I think I'm getting there.

One more time.

A capacitor consists of two separate conductors with a potential difference between them. Look at the schematic of a capacitor connected to a battery. The dotted lines enclose two separate conductors at separate potentials, red higher than black.

Here you have a single conductor with charges separated at its ends.

 

[Juanda]

All right. Now the click was significantly louder in my head. I thought you were doing the emphasis on the difference in proximity of the two plates in the different cases and I was not getting what was so fundamentally different about it.
If the battery separates the circuit like that to cause the jump in voltage and you say that is inherently different from the difference in potential caused by the induced voltage then I will accept it.

What would the associated circuit be then though? When the circuit is closed as in the initial post, the current can flow and it dissipates energy. That case is crystal clear. The induced voltage can be drawn "equivalent" to a battery and the resistance is that of the conductor itself and other external resistances if installed.

What about this case with just the rod?

• Initial conditions: Starting from a stop and no charge yet accumulated.
• Then a force is applied. Imagine me pushing the rod with my hand.
• The rod picks up speed.
• The speed and the magnetic field cause the electrons to move to one end of the rod. During that movement, some energy is dissipated as heat like in a normal resistance. The remaining energy accumulates in the rod as potential energy.
• I now keep pushing with my hand in any way necessary so the speed remains constant. Then, the magnetic field will no longer apply a drag force because there is no current flowing on it. The charges are already bunched up from before so the induced voltage is in equilibrium.
• Now I increase the force done by my hand. The rod will accelerate to a new velocity which has a new induced voltage associated with it. The rod will again suffer a drag force as the current flows to reach the new induced voltage associated with the new velocity.

I believe that whenever the charges are moving to bunch up I should feed a drag force. Even if there were no dissipation in the form of heat.

If it is not a capacitor with a resistance in series, how could I model it? I suggested a capacitor because the charges were bunching up and generating an electric field across the air but it seems that's not the right approach.
I would like to be able to link the equations of Newton and the equations from this "circuit" so that the dynamics of the system are defined.
Again, I can move this to the electromagnetism section if this is not the right place to discuss it.


PS: Nice formatting with the picture on the side. I had never seen it here. How did you do it? I remember there is a way to see what you wrote instead of what the forum shows. Kind of like using ## or $$ when writing equations but I forgot how to do it.

 

[kuruman]

There is no need to move this thread to electromagnetism. It's still classical physics.

You worry too much about the accumulation of charges at the ends. There no transport current and no $I\mathbf{L}\times\mathbf{B}$ force to speak of. Think of it as redistribution of charges in response to changes in an electric field external to the conductor. This redistribution occurs near instantly. The drag force will be gone before the nerve impulse that the force has changed reaches your brain. The time scale is less than a microsecond.

To put a picture on the side. You already know how to embed a picture in the post. To move a picture
1. Click on it to pop the figure options menu

2. Click on the down arrow on the left to pop the placement options menu

3. Choose one of the three
Top: Justify left.
Middle (Highlighted): Justify center
Bottom: Justify right.

Have fun.

 

[Juanda]

All right. I will let it go then. I will assume that in such a scenario the induced voltage happens but the rod acts in the same way as if there wasn't a magnetic field to start with in terms of dynamics.
Following that logic, if I had a solid disc rotating inside a constant magnetic field (Faraday motor / Homopolar generator), it would not feel any drag at all. Charges would bunch up similarly as with the previously discussed rod but there would be no drag since there is no significant current. Only if the circuit is closed connecting the outer edge to the center the current would start flowing and drag would show up. Is that correct?

 

[kuruman]

That is correct. You need to do work on the generator to overcome the drag and keep it going. If you didn't, you would have a very cheap source of electrical energy. The homopolar generator is sufficiently different from what we have been discussing here to warrant a new thread. So start one if you wish to explore it further.

 

[Juanda]

I most likely will. I will try it tomorrow.
Although probably it will be focused on Eddy Current Dampers. Thank you for the support so far.