Confusion regarding signs in SHM problem

[Tanya Sharma]

Homework Statement

A spherical ball of mass M and radius r rolls without slipping in a cylindrical of radius R .Find the time period of small oscillations .

Homework Equations

The Attempt at a Solution

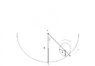
Please have a look at the picture attached .

The ball moves to the right and upward, and rotates about its centre clockwise . $\phi$ is the angle from the vertical by which the ball has turned .$\theta$ is the angular displacement of the CM of the ball.

$\ddot{\theta}$ is the angular acceleration of the CM of the ball about the center of the curve .

$\ddot{\phi}$ is the angular acceleration of the ball about its CM .

Considering anticlockwise as positive and rightwards as positive .

Equation for the motion of the CM :

$f_s - Mgsin\theta = Ma$

Equation for the rotation about the CM

$f_sr = -I\ddot{\phi}$

Rolling without slipping condition :

$a=\ddot{\phi}r$

Constraint equation :

$\ddot{\phi}r = (R-r)\ddot{\theta}$

Solving the above gives the correct time period .

Ok till here but if I consider the ball rolling down from right towards A , I get confused with the signs in the first two equations.

1) Even though I have written the correct torque equation $f_sr = -I\ddot{\phi}$ , I am not quite confident with the reasoning I had regarding the negative sign on the RHS . Is it because $\phi$ is increasing clockwise and I have taken anticlockwise as positive Or is it because $\ddot{\phi}$ is decelerating the rotation ?

2) How do I determine the sign of $\ddot{\phi}$ and $\ddot{\theta}$ ?

3) How should I modify the first two equations ?

 

[TSny]

Ok till here but if I consider the ball rolling down from right towards A , I get confused with the signs in the first two equations.

1) Even though I have written the correct torque equation $f_sr = -I\ddot{\phi}$ , I am not quite confident with the reasoning I had regarding the negative sign on the RHS . Is it because $\phi$ is increasing clockwise and I have taken anticlockwise as positive Or is it because $\ddot{\phi}$ is decelerating the rotation ?

Hello, Tanya.
It seems to me that you have taken clockwise as positive for $\phi$ and counterclockwise positive for $\theta$. Note that your equation $\ddot{\phi}r = (R-r) \ddot{\theta}$ implies $\phi r = (R-r) \theta$. This implies that you have chosen positive directions so that $\phi$ increases as $\theta$ increases.

2) How do I determine the sign of $\ddot{\phi}$ and $\ddot{\theta}$ ?

I'm not quite sure what you are asking here? Are you asking how to determine what sign goes in front of these symbols when setting up an equation? Or are you asking how to determine if the quantity $\ddot{\phi}$, say, is itself a positive or negative quantity?

3) How should I modify the first two equations ?

Why do you think you would need to modify the equations for when the ball is rolling back down? If you throw a ball straight up, the equation $\ddot{y} = -g$ holds for going up and for coming down.

 

[Tanya Sharma]

Hello TSny

Thanks for replying .

Note that your equation $\ddot{\phi}r = (R-r) \ddot{\theta}$ implies $ϕr=(R−r)θ$.

I thought ,since this was a constraint equation , we need to deal only with the magnitudes .Hence I didn't put any sign . When would we need to write it as $\ddot{\phi}r = -(R-r) \ddot{\theta}$ ?

Do we need to consider signs in no slip condition $a=\ddot{\phi}r$ as well ?

Sorry , but I am super confused .

I'm not quite sure what you are asking here? Are you asking how to determine what sign goes in front of these symbols when setting up an equation?

Yes .

 

[TSny]

You do need to consider signs when setting up constraint equations.

You do not have to choose the positive direction in the same way for both angles. In this problem, I think it's nice to take counterclockwise as positive for $\theta$ and clockwise positive of $\phi$. Then, when the sphere is rolling up to the right, both $\theta$ and $\phi$ are increasing. This agrees with the way you wrote the constraint.

If you choose counterclockwise as positive for both angles, then you would need to include the negative sign in the constraint since $\ddot{\phi}$ would be negative when $\ddot{\theta}$ is positive.

When setting up an equation such as a torque equation you would just write $\sum \tau = I\ddot{\phi}$. This would be valid whether $\ddot{\phi}$ itself is positive or negative and whether you took positive direction for $\phi$ as clockwise or counterclockwise. If you have taken clockwise as positive direction for $\phi$, then you would need to interpret clockwise torques as positive.

 

[Tanya Sharma]

You do need to consider signs when setting up constraint equations.

Ok . Do we consider no slip condition as a constraint equation i.e do we need to take care of the signs in it as well ?

If you choose counterclockwise as positive for both angles, then you would need to include the negative sign in the constraint since $\ddot{\phi}$ would be negative when $\ddot{\theta}$ is positive.

How do we determine whether $\ddot{\phi}$ and $\ddot{\theta}$ are positive or negative ?

When setting up an equation such as a torque equation you would just write $\sum \tau = I\ddot{\phi}$. This would be valid whether $\ddot{\phi}$ itself is positive or negative and whether you took positive direction for $\phi$ as clockwise or counterclockwise. If you have taken clockwise as positive direction for $\phi$, then you would need to interpret clockwise torques as positive.

Why are we concerned with the sign of torque only and not of $\ddot{\phi}$ and $\phi$ ?

 

[TSny]

Ok . Do we consider no slip condition as a constraint equation i.e do we need to take care of the signs in it as well ?

Yes, you need to worry about signs in this equation also.

How do we determine whether $\ddot{\phi}$ and $\ddot{\theta}$ are positive or negative ?

It depends on your choice of positive direction and where the sphere is at the moment. When the sphere is on the right side of the cylinder (either rolling up or back down) $\ddot{\theta}$ will be negative if you have chosen counterclockwise as positive for $\theta$. But, you do not need to worry about this when setting up the torque equations.

For example, for a particle moving along the x-axis, you would write $\sum F_x = m \ddot{x}$ without worrying about whether $\ddot{x}$ happens to be positive or negative at the instant of time you are applying the equation.

Why are we concerned with the sign of torque only and not of $\ddot{\phi}$ and $\phi$ ?

If you choose clockwise as positive direction for $\phi$, then a clockwise torque would be considered positive.
Thus, if you have taken the positive direction for the friction force $f$ to be up along the slope when the ball is on the right side, then the torque due to $f$ would be counterclockwise. Since you have chosen clockwise as the positive direction for $\phi$, the friction torque would be written $-fr$ when substituting into $\sum \tau = I \ddot{\phi}$. If you then move the negative sign to the other side, you get the equation that you used in your first post.

 

[Tanya Sharma]

It depends on your choice of positive direction and where the sphere is at the moment. When the sphere is on the right side of the cylinder (either rolling up or back down) $\ddot{\theta}$ will be negative if you have chosen counterclockwise as positive for $\theta$.

But then , since clockwise is positive for $\phi$ ,when the sphere is on the right side of the cylinder (either rolling up or back down) $\ddot{\phi}$ will be negative ?

 

[TSny]

Yes.

 

[Tanya Sharma]

And acceleration 'a' is also negative when the sphere is on the right side of the cylinder (either rolling up or back down) ?

 

[TSny]

$a$ is a negative quantity when the sphere is on the right side if you have chosen the positive direction of translation to be toward the right.
But that doesn't mean that you would write a negative sign in front of $a$ when setting up $\sum F = ma$.

 

[Tanya Sharma]

So the rules are

1) We consider signs of $a$ , $\ddot{\phi}$ and $\ddot{\theta}$ while writing constraint equations .
2) We consider signs of only forces and torques while writing force and torque equations .

Right ?

 

[TSny]

For (2), I would say yes.

For (1) I would say "ok, sort of ". Constraints are relations between kinematic quantities. The important thing is to get the relation right. If two quantities are proportional but one quantity is negative whenever the other is positive, then you need a negative constant of proportionality.

 

[Tanya Sharma]

"ok, sort of "

So ,irrespective of whether the sphere is towards left or right , whether rolling up or down , the four equations written in post#1 remain as it is .

Sounds okay ?

 

[TSny]

Well, you need to be careful. (Sorry.) If you define the symbol $f_s$ to represent the magnitude of the friction force (thus, the symbol always denotes a positive quantity), then you will need to modify slightly the first two equations when the sphere is on the left. But you will still be led to the same result when combining the equations.

If, instead, you let $f_s$ denote the component of force tangent to the slope toward the counterclockwise direction, then it will be a negative quantity when the sphere is on the left. Then the equations are the same for the sphere on the left and right.

Either way, when combining the equations you will still end up with the same differential equation of motion.

You can see how everything depends on how you wish to define your symbols. Don't let them push you around! You're the master. You get to decide on whatever conventions you want. But it's your responsibility to keep everything consistent with your choices.

We all have trouble with signs. I mess them up all the time.

 

[Tanya Sharma]

We all have trouble with signs. I mess them up all the time.

Are you sure about the last three words ? I think you intended to write " once in a while " .

Suppose the ball moves to the right and upward, and rotates about its centre clockwise . But now we take clockwise positive for both $\phi$ and $\theta$ and leftwards positive. I have a doubt here as $\theta$ is being measured from the vertical and is increasing counterclockwise . Can we even consider clockwise positive for $\theta$ ? I am unsure .

In this case $\ddot{\theta}$ is positive and $\ddot{\phi}$ is negative . Right ??

The equations formed would be

$Mgsin\theta -f_s = Ma$

$-f_sr = I\ddot{\phi}$

$a=-\ddot{\phi}r$

$-\ddot{\phi}r = (R-r)\ddot{\theta}$

Where is the mistake ?

Please forgive me if I have done something stupid (as I have been doing repeatedly).

 

[TSny]

Suppose the ball moves to the right and upward, and rotates about its centre clockwise . But now we take clockwise positive for both $\phi$ and $\theta$ and leftwards positive. I have a doubt here as $\theta$ is being measured from the vertical and is increasing counterclockwise . Can we even consider clockwise positive for $\theta$ ?

Yes, certainly. (Feel the power!)

In this case $\ddot{\theta}$ is positive and $\ddot{\phi}$ is negative . Right ??

That's right.

The equations formed would be

$Mgsin\theta -f_s = Ma$

If toward the left is now positive direction, then your gravity force has the wrong sign. Note that $\theta$ is negative when the ball is on the right.

$-f_sr = I\ddot{\phi}$

$a=-\ddot{\phi}r$

$-\ddot{\phi}r = (R-r)\ddot{\theta}$

These look good.