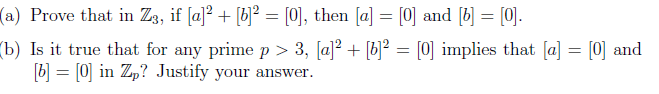Congruence Class Proofs: Tips and Examples
Click For Summary
The discussion focuses on congruence class proofs within the context of modular arithmetic, specifically in the ring $\mathbb{Z}_{3}$. Key insights include the simplification of expressions by representing elements as $[a] = 3n + a$ and $[b] = 3m + b$, leading to the conclusion that for $[a]^2 + [b]^2 = 0$, both $a$ and $b$ must equal 0. The participants emphasize the importance of considering cases and recognizing that the results of squaring in $\mathbb{Z}_{3}$ yield only $[0]$ or $[1]$. This leads to a streamlined approach to proving congruences.
PREREQUISITES- Understanding of modular arithmetic, specifically $\mathbb{Z}_{3}$
- Familiarity with congruence classes and their properties
- Basic algebraic manipulation involving polynomials
- Knowledge of mathematical proofs and counterexamples
- Study the properties of $\mathbb{Z}_{n}$ for various values of n
- Learn about polynomial congruences and their applications
- Explore the concept of equivalence relations in mathematics
- Investigate the use of counterexamples in mathematical proofs
Students and educators in mathematics, particularly those focusing on abstract algebra and number theory, as well as anyone interested in enhancing their proof-writing skills in modular arithmetic.
Similar threads
- · Replies 17 ·
- · Replies 2 ·
- · Replies 2 ·
- · Replies 12 ·
- · Replies 17 ·
- · Replies 2 ·
- · Replies 3 ·