Connection of zeta to primes: less Euler than error or L-functions?

[nomadreid]

TL;DR

The connection between the Riemann zeta function and primes is often stated as lying in Euler's product formula, but wouldn't it be more correct that it lies in the zeta function role in the error function for the prime number theorem, or perhaps the explicit formulas of L-functions?

Often I read that the Riemann Hypothesis (RH) is related to prime numbers because of the equivalence on Re(s)>1 of the zeta function and Eurler's product formula

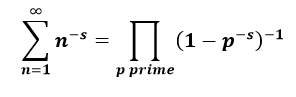
, but is it more accurate that the relevance of the RH to primes (or vice-versa) is either that the RH implies formulas for the error terms of the prime number theorem, for example, the von Koch/Schoenfeld's

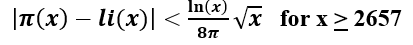
(as given in https://en.wikipedia.org/wiki/Riemann_hypothesis#Distribution_of_prime_numbers)

or even more so that the ρ in some of the explicit formulas for L-functions ranges over the non-trivial zeros of the Riemann zeta function (as outlined in https://en.wikipedia.org/wiki/Explicit_formulae_for_L-functions#Riemann's_explicit_formula)?

Or do the latter two results simply hark back to the Euler result in some way?

 

[Infrared]

In general, all of relationships between the zeta function and distribution of primes come from the Euler product. Exactly how depends on which identity you want, but the general idea is that you take the logarithmic derivative of the Euler product and perform contour integration. The further you can push the region of integration to the left, the better estimates you get, which is why the Riemann hypothesis would imply a smaller error term in the prime number theorem (since if RH is true, then $\zeta'/\zeta$ doesn't have any poles until you reach the line of real part $1/2$).

 

[nomadreid]

Thank you, Infrared. Excellent explanation.