Cons. of energy with rotational motion

[musicfairy]

In Figure 11-32, a solid brass ball of mass m and radius r will roll without slipping along the loop-the-loop track when released from rest along the straight section. For the following answers use g for the acceleration due to gravity, and m, r, and R, as appropriate, where all quantities are in SI units.

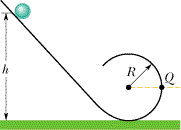
(a) From what minimum height h above the bottom of the track must the marble be released to ensure that it does not leave the track at the top of the loop? (The radius of the loop-the-loop is R. Assume R > r.)

(b) If the marble is released from height 6R above the bottom of the track, what is the magnitude of the horizontal component of the force acting on it at point Q?



For part a I came up with the equation

mgh = (1/2)mv² + (1/2)mv² + 2mgR
gh = (7/10)v² + 2gR

I think that's right, but I can't figure out how to solve for v. I'm guessing that It has something to do with centripetal force.


Part b probably needs an answer from part a. The horizontal component of the force is the normal force (= centripetal force?).

Help please.

 

[curly_ebhc]

your logic is good (except I don't get your second 1/2mv2).

You are right about centripetal force. At the top the ball needs enough velocity so that its centripetal inertia= its weight. The force of gravity must equal its centripetal force. This will translate directly into an equation for velocity from centripetal acceleration or froce.

 

[Doc Al]

For part a I came up with the equation

mgh = (1/2)mv² + (1/2)mv² + 2mgR
gh = (7/10)v² + 2gR

OK. (That second term in your first equation should be rotational KE.)

I think that's right, but I can't figure out how to solve for v. I'm guessing that It has something to do with centripetal force.

Right. Apply Newton's 2nd law to solve for v.

Part b probably needs an answer from part a.

Not really.

The horizontal component of the force is the normal force (= centripetal force?).

Yep.

 

[musicfairy]

For that I meant to say 1/5mv²

For part a I set N = 0 at the top of the loop

N + mg = mv²/(R-r)

g = v²/(R-r)

v² = g(R-r)

gh = (7/10)g(R-r) + 2gR

h = (7/10)g(R-r) + 2R




Part b

Using the equation from earlier...

g(6R) = (7/10)v² + gR
v² = (50/7)gR

N = mv² / (R-r)
N = m(50gR)/(7(R-r))



But it won't take my answer. =(


What did I do wrong now?

 

[Doc Al]

For that I meant to say 1/5mv²

For part a I set N = 0 at the top of the loop

N + mg = mv²/(R-r)

g = v²/(R-r)

v² = g(R-r)

gh = (7/10)g(R-r) + 2gR

h = (7/10)g(R-r) + 2R

The height of the ball's center at the top of the motion should be 2R-r, not 2R.

Part b

Using the equation from earlier...

g(6R) = (7/10)v² + gR
v² = (50/7)gR

N = mv² / (R-r)
N = m(50gR)/(7(R-r))

This looks OK to me.