- #1
Pochen Liu
- 52
- 2
Homework Statement
This question is referring to the classic ball in a loop question where it is dropped from a height and slides into a loop de loop.
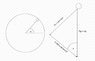
Derive an expression in terms of theta the velocity of the ball at the time it loses contact with the track. Theta is measured from the horizontal at the height of the radius (Like the unit circle). And I am deeply struggling with this explanation
The ball will leave the rail when the rail reaction is zero. This happens when the centripetal force needed to travel around the loop is totally supplied by the component of the gravity force directed towards the centre of the motion.
I'm fine with the concept of working out the minimal velocity it needs so that the ball doesn't loose contact with the track v = sqrt(rg) because Fc and Fg are acting in the same direction
however how is the Fg acting along the radial part? It makes no sense to me as gravity should only act downwards in one direction not towards the center of the circle
Homework Equations
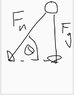
mg*sin(theta) = mv2/r - this is the equation I am struggling with, why is sin(theta) on the mg side
The Attempt at a Solution
My reasoning is that Fn vertical component when equal to Fg will start to fall, so if i draw a vector diagram and take out the vertical component of Fc/Fn
(mv2/r) * sin(theta) = mg
Can someone point out the fatal flaw in my intuition?