Conservation of Angular momentum problem

[i_hate_math]

Homework Statement

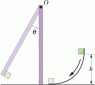
In the figure, a small 0.235 kg block slides down a frictionless surface through height h = 0.471 m and then sticks to a uniform vertical rod of mass M = 0.470 kg and length d = 2.36 m. The rod pivots about point Othrough angle θ before momentarily stopping. Find θ.

Homework Equations

L=I*w
P=mv
v=wr
Ki=Kf -----> 0.5mv^2=mgh , and this gives expression for 'v'
w^2=w0^2 + 2*alpha*(delta ø) , for when alpha(angular acceleration) is constant

The Attempt at a Solution

in effort to find ø, alpha and w are needed. I established that m*v=I*w (not sure if this is correct)

by substituting relevant equations, i got w0=[sqrt(2gh)]/d^2
and w, is according to the question, 0.

now i can't seem to find an expression for alpha.
could u point out what i missed out?

 

[Let'sthink]

Find out angular momentum of the system just after impact. Just before the impact the angular momentum is non-zero only for the hitting block given by mvr*L about the pivot, which moment of momentum. Assume some instantaneous velocity V for the hit tip of the rod, which will be the same for the block too just after it sticks.. Your equation is wrong even dimension-ally.

 

[haruspex]

when alpha(angular acceleration) is constant

But it won't be.

 

[Let'sthink]

Because alpha is not constant you cannot apply that formula. Apply Total L conservation just before and after impact and for rest segments apply energy conservation.

 

[i_hate_math]

Find out angular momentum of the system just after impact. Just before the impact the angular momentum is non-zero only for the hitting block given by mvr*L about the pivot, which moment of momentum. Assume some instantaneous velocity V for the hit tip of the rod, which will be the same for the block too just after it sticks.. Your equation is wrong even dimension-ally.

I've reworked an expression for w, w=sqrt(2gh)/3d
by applying I*w = I*w
but then how do i find the angle?

 

[haruspex]

sqrt(2gh)/3d

I don't understand how you get that. Please post your working.

 

[kinemath]

why isn't alpha constant?

 

[haruspex]

I don't understand how you get that. Please post your working.

What force is responsible for the angular acceleration? Is its moment about the centre of the arc constant?

 

[kinemath]

Oh I get it thanks a lot.
Is it because gravity causes the tangential force to change when the rod pivots which causes the angular acceleration to change?

 

[haruspex]

Oh I get it thanks a lot.
Is it because gravity causes the tangential force to change when the rod pivots which causes the angular acceleration to change?

Yes, as the angle changes the tangential component of gravity changes.

 

[Let'sthink]

Because Torque acting on the bar and the attached piece is not constant.

 

[i_hate_math]

I don't understand how you get that. Please post your working.

Right before the cube collied with the rod, it's angular moment is I*w=1/3md^2 * (v/d), where v=(2gh)^0.5
right after the collision, the new I*w=1/3(m+M)d^2 * w

now that I*w=I*w, we have new w=(mv)/(m+M)d=(1/3)(v/d)=sqrt(2gh)/3d

 

[haruspex]

Right before the cube collied with the rod, it's angular moment is I*w=1/3md^2 * (v/d)

It is described as small, so consider it a point particle. Where do you get the 1/3 from?

 

[i_hate_math]

It is described as small, so consider it a point particle. Where do you get the 1/3 from?

m/(m+M)=0.235/(0.235+0.47)=1/3

 

[haruspex]

m/(m+M)=0.235/(0.235+0.47)=1/3

I still don't get it. You wrote

Right before the cube collided with the rod, it's angular moment is

so we're talking about the angular momentum of the small block. It has not hit the rod yet, so M cannot play a role.

 

[i_hate_math]

I still don't get it. You wrote

so we're talking about the angular momentum of the small block. It has not hit the rod yet, so M cannot play a role.

I assumed it could as suggested by the other guy

Because alpha is not constant you cannot apply that formula. Apply Total L conservation just before and after impact and for rest segments apply energy conservation.

If this does not hold, which equation shall I establish?

 

[haruspex]

I assumed it could as suggested by the other guy

Do you mean this:

Find out angular momentum of the system just after impact. Just before the impact the angular momentum is non-zero only for the hitting block given by mvr*L about the pivot,

If so, you are misreading it. The expression for the angular momentum of the block just before impact is clearly stated there. But the first part, "Find out angular momentum of the system just after impact." may be slightly misleading. Let'sthink means the angular momentum of block+rod just after impact (and this does involve M) is equal to that of the block just before impact. So you need two expressions for angular momentum, one just before impact and one just after, which you then set equal to obtain an equation.

If this does not hold, which equation shall I establish?

You do not need to worry about forces and accelerations. Just use conservation laws as appropriate. After impact, what is conserved?

 

[i_hate_math]

Do you mean this:

If so, you are misreading it. The expression for the angular momentum of the block just before impact is clearly stated there. But the first part, "Find out angular momentum of the system just after impact." may be slightly misleading. Let'sthink means the angular momentum of block+rod just after impact (and this does involve M) is equal to that of the block just before impact. So you need two expressions for angular momentum, one just before impact and one just after, which you then set equal to obtain an equation.

You do not need to worry about forces and accelerations. Just use conservation laws as appropriate. After impact, what is conserved?

So the angular momentum of the small block would be I*w of the slide-block system, I=(1/3)mh^2, w=v/r

 

[haruspex]

So the angular momentum of the small block would be I*w of the slide-block system, I=(1/3)mh^2, w=v/r

Forget the rod for the moment. We have a small block which has reached a speed of √(2gh) and is traveling horizontally at a distance d below point O. What is the angular momentum of the block about point O? If you think there is a factor 1/3 in the answer, please explain how you arrive at that.

 

[i_hate_math]

Forget the rod for the moment. We have a small block which has reached a speed of √(2gh) and is traveling horizontally at a distance d below point O. What is the angular momentum of the block about point O? If you think there is a factor 1/3 in the answer, please explain how you arrive at that.

Oh right, so L=r*p where p=m*v, thus L=r*m*v=h*sqrt(mgh)*m

 

[haruspex]

r*m*v=h*sqrt(mgh)*m

Too many h's, too many m's. What is r here? Is one of the m's a typo?

 

[i_hate_math]

Too many h's, too many m's. What is r here? Is one of the m's a typo?

soz, r=h v=sqrt(mgh) and the block has mass m.
thus L=r*p=rmv=h*m*sqrt(mgh)

 

[haruspex]

r=h

Wrong.

v=sqrt(mgh)

Wrong again (even, dimensionally wrong).

 

[i_hate_math]

Wrong.

Wrong again (even, dimensionally wrong).

v=sqrt(2gh). but why isn't r=h?

 

[haruspex]

v=sqrt(2gh). but why isn't r=h?

Because we're discussing the angular momentum about point O, i.e. the top of the rod. How the particle came to be traveling horizontally at this speed is no longer of interest, so h plays no further part (beyond determining the speed).

 

[i_hate_math]

Because we're discussing the angular momentum about point O, i.e. the top of the rod. How the particle came to be traveling horizontally at this speed is no longer of interest, so h plays no further part (beyond determining the speed).

shall i replace h with d?

 

[haruspex]

shall i replace h with d?

Yes.

 

[i_hate_math]

Yes.

okay, then I have w=sqrt(mgh)/d
could u suggest a way to find the angle ø?(I haven't learned this chapter of physics course yet, limited knowlege)

 

[haruspex]

then I have w=sqrt(mgh)/d

No. Reread your own post #24.

could u suggest a way to find the angle ø?

Reread the last lines of posts #4 and #17.

 

[i_hate_math]

No. Reread your own post #24.

Reread the last lines of posts #4 and #17.

w=sqrt(2gh)/d

use energy conservation, so delta(GPE)=1/2Iw^2?

 

[haruspex]

w=sqrt(2gh)/d

use energy conservation, so delta(GPE)=1/2Iw^2?

Right. The final challenges are to calculate I correctly for the rod plus block, and express the ΔGPE as a function of the angle.

 

[i_hate_math]

okay,
now w=sqrt(mgh)/d
mgl=0.5Iw^2, where l is change in height
and by subing in all the mess l=h
and then ø=arccos[(d-h)/d]=36.8

 

[i_hate_math]

okay,
now w=sqrt(mgh)/d
mgl=0.5Iw^2, where l is change in height
and by subing in all the mess l=h
and then ø=arccos[(d-h)/d]=36.8

soz w=sqrt(2gh)/d i meant

 

[kinemath]

l is not equal to h

 

[i_hate_math]

l is not equal to h

I mean after subing in all the values, i got l=h, or did i do the wrong calculations?