alkaspeltzar
- 354
- 37
- TL;DR
- Looking for clarity on how kinetic energy is conserved in an assume elastic collision between a moving wedge and stationary ball, looking at the work and energy transfer.
So assume we have a wedge traveling at a constant V horizontally, that is braced so it CANNOT move vertically. Ignore air and friction. See picture.
It hits a stationary tennis ball and due to the angle, there is a net force on the ball as shown.
The energy should come from the kinetic energy of the wedge. However, if i were to look at the Work of the the horizontal reaction force on the wedge over the distance(wedge slows and loses energy), wouldn't the ball have the same force horizontally, over the same distance PLUS the work done from vertical component? what am i missing as that would be more energy right?
Only thing i can think of it that both items deform, and thru their deformation, the energy is stored as potential and then back to kinetic energy. As such both the energy lost of the wedge is equal to that of the ball. Trying to break it down is going to cause confusion.
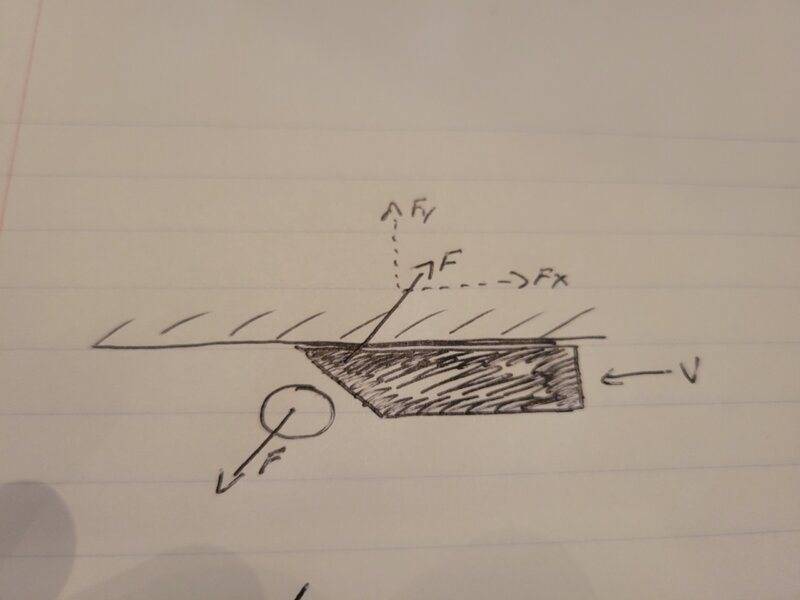
It hits a stationary tennis ball and due to the angle, there is a net force on the ball as shown.
The energy should come from the kinetic energy of the wedge. However, if i were to look at the Work of the the horizontal reaction force on the wedge over the distance(wedge slows and loses energy), wouldn't the ball have the same force horizontally, over the same distance PLUS the work done from vertical component? what am i missing as that would be more energy right?
Only thing i can think of it that both items deform, and thru their deformation, the energy is stored as potential and then back to kinetic energy. As such both the energy lost of the wedge is equal to that of the ball. Trying to break it down is going to cause confusion.