Conservation of momentum and angular momentum

[Eitan Levy]

Homework Statement

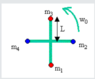
4 masses attached by a cross with no mass are spinning on a smooth table around the center of the cross. The distance between any mass to the center is L. The angular velocity is ω₀.
m₁=m₃,m₂=m₄

Suddenly, at t=0 (the time described in the picture), m₄ disconnects from the cross.

Find the linear velocity of the cross after it disconnects.

Find the angular velocity of the three masses left around their center of mass.

Homework Equations

J=RxP
P=mv

The Attempt at a Solution

I am having a hard time figuring out what sizes will be conserved and why. Assuming the mass disconnects without any force involved, both the linear momentum and the angular momentum are supposed to be conserved in the system of the four masses.

On the other hand, when the cross will be spinning from this point, no external forces/torques will affect the three masses left, so they are supposed to be conserved there too.

I can't figure out how it's possible to get an answer, if all those sizes are conserved (I am not really sure they will but can't understand why not) I get stuck with equations with no solutions. How is it possible to get an answer if the momentum in the three mass system is conserved throughout its spin?

Thanks a lot.

 

[Charles Link]

There are never any external torques, so the total angular momentum of the system remains conserved. $\\$ Mass 4, if I'm not mistaken, still has an angular momentum that should be the same value as when it was attached, because no external torques were applied while it was released or afterwards. Meanwhile, when the 4 attached masses are spinning at a constant rate, each has a constant angular momentum, since the only force (centripetal) is along $\vec{r}$ so that torque $\tau=\vec{r} \times \vec{F} =0$ for each of the masses. $\\$ Here's a hint for you: Use as a rest frame the laboratory with origin at the center of the cross when it had the 4 masses attached. Compute the angular momentum of mass 4, $\vec{L}_4=\vec{r} \times \vec{p}$, at the instant it is released, as measured from this inertial laboratory frame. Does this number change? Compute it at a later time $t$. What then must be the angular momentum of the 3 remaining attached masses? $\\$ I think this problem might have an extra degree of difficulty in calculating the rotational rate, because the 3 connected masses will have an angular momentum if they are just moving at a constant velocity and not rotating. The angular momentum from the rotational motion needs to add to the angular momentum measured from the inertial laboratory frame from the linear motion of the system of the 3 connected masses. Note: $\vec{L}_{1,2,3 \, translational} =\vec{r} \times \vec{p}_{center \, of \, mass} \neq 0$, and must be included in the conservation equations for angular momentum $\vec{L}$. And the number for the angular velocity of the 3 masses is a tricky one, because in order to compute $\vec{ \omega}$ for this system, I think you need to compute the moment of inertia $I$. Once you have that, and know what $\vec{L}_{1,2,3 \, rotational}$ needs to be, then you can compute $\vec{\omega}=\frac{\vec{L}_{1,2,3 \, rotational}}{I}$. Anyway, that's how I believe it needs to be worked. $\\$ ( Note: This one is slightly more advanced than most angular momentum calculations that I have previously seen). $\\$ Edit: Additional note: The $\vec{L}_{rotational}$, I believe is the same, whether it is measured in the laboratory frame or in the center of mass frame. Your textbook should have a theorem about this, but I believe that to be the case.

 

[Eitan Levy]

There are never any external torques, so the total angular momentum of the system remains conserved. $\\$ Mass 4, if I'm not mistaken, still has an angular momentum that should be the same value as when it was attached, because no external torques were applied while it was released or afterwards. Meanwhile, when the 4 attached masses are spinning at a constant rate, each has a constant angular momentum, since the only force (centripetal) is along $\vec{r}$ so that torque $\tau=\vec{r} \times \vec{F} =0$ for each of the masses. $\\$ Here's a hint for you: Use as a rest frame the laboratory with origin at the center of the cross when it had the 4 masses attached. Compute the angular momentum of mass 4, $\vec{L}_4=\vec{r} \times \vec{p}$, at the instant it is released, as measured from this inertial laboratory frame. Does this number change? Compute it at a later time $t$. What then must be the angular momentum of the 3 remaining attached masses? $\\$ I think this problem might have an extra degree of difficulty in calculating the rotational rate, because the 3 connected masses will have an angular momentum if they are just moving at a constant velocity and not rotating. The angular momentum from the rotational motion needs to add to the angular momentum measured from the inertial laboratory frame from the linear motion of the system of the 3 connected masses. Note: $\vec{L}_{1,2,3 \, translational} =\vec{r} \times \vec{p}_{center \, of \, mass} \neq 0$, and must be included in the conservation equations for angular momentum $\vec{L}$. And the number for the angular velocity of the 3 masses is a tricky one, because in order to compute $\vec{ \omega}$ for this system, I think you need to compute the moment of inertia $I$. Once you have that, and know what $\vec{L}_{1,2,3 \, rotational}$ needs to be, then you can compute $\vec{\omega}=\frac{\vec{L}_{1,2,3 \, rotational}}{I}$. Anyway, that's how I believe it needs to be worked. $\\$ ( Note: This one is slightly more advanced than most angular momentum calculations that I have previously seen).

There are never any external torques, so the total angular momentum of the system remains conserved. $\\$ Mass 4, if I'm not mistaken, still has an angular momentum that should be the same value as when it was attached, because no external torques were applied while it was released or afterwards. Meanwhile, when the 4 attached masses are spinning at a constant rate, each has a constant angular momentum, since the only force (centripetal) is along $\vec{r}$ so that torque $\tau=\vec{r} \times \vec{F} =0$ for each of the masses. $\\$ Here's a hint for you: Use as a rest frame the laboratory with origin at the center of the cross when it had the 4 masses attached. Compute the angular momentum of mass 4, $\vec{L}_4=\vec{r} \times \vec{p}$, at the instant it is released, as measured from this inertial laboratory frame. Does this number change? Compute it at a later time $t$. What then must be the angular momentum of the 3 remaining attached masses? $\\$ I think this problem might have an extra degree of difficulty in calculating the rotational rate, because the 3 connected masses will have an angular momentum if they are just moving at a constant velocity and not rotating. The angular momentum from the rotational motion needs to add to the angular momentum measured from the inertial laboratory frame from the linear motion of the system of the 3 connected masses. Note: $\vec{L}_{1,2,3 \, translational} =\vec{r} \times \vec{p}_{center \, of \, mass} \neq 0$, and must be included in the conservation equations for angular momentum $\vec{L}$. And the number for the angular velocity of the 3 masses is a tricky one, because in order to compute $\vec{ \omega}$ for this system, I think you need to compute the moment of inertia $I$. Once you have that, and know what $\vec{L}_{1,2,3 \, rotational}$ needs to be, then you can compute $\vec{\omega}=\frac{\vec{L}_{1,2,3 \, rotational}}{I}$. Anyway, that's how I believe it needs to be worked. $\\$ ( Note: This one is slightly more advanced than most angular momentum calculations that I have previously seen).

Thanks for the reply! We were given this problem before we learned about the moment of inertia so I doubt this should be used. I believe that L₄ doesn't change, however I am still stuck.

 

[Charles Link]

Thanks for the reply! We were given this problem before we learned about the moment of inertia so I doubt this should be used. I believe that L₄ doesn't change, however I am still stuck.

Please see the "Edit: Additional note" above. (bottom of post 2) $\\$ Perhaps this one has a simple solution, but from what I can tell, it is a somewhat advanced problem.

 

[Eitan Levy]

Please see the "Edit: Additional note" above. (bottom of post 2) $\\$ Perhaps this one has a simple solution, but from what I can tell, it is a somewhat advanced problem.

I agree that it should be the same, using J=J_CM+R_CMxP_CM (V_CM=0 so P_CM=0). How do I use that to reach the velocity in the first question though?

I am trying to think how the system has changed and what will cause that linear velocity. The problem originally came with numbers, but the answer is equal to m₄ω₀r/(m₁+m₂+m₃ (Which equals to my original guess, but then I could not understand how to reach that). I think it is supposed to be a more simple problem, because I have solved ones that should be harder (questions ranked by difficulty), but I think that what makes you think it is a more advanced problem is confusing me as well, because I am not sure what assumptions should be made. A lot of students had trouble with this problem specifically.

The masses are: m₁=m₃=4kg, m₂=m₄=8kg and the linear velocity is 3m/s. Does that help?

 

[Charles Link]

To get the linear velocity of the center of mass of the 3 coupled masses, you simply need conservation of the linear momentum, using $(m_1+m_2+m_3) \vec{v}_{cm} + m_4 \vec{v}_4=0$. $\\$ And $\vec{v}_{cm}$ will be upward. $\\$ Once you have that, you need to find the location of the center of mass (for the 3 connected masses) in order to compute $L_{1,2,3 \, translational}=\vec{r} \times \vec{p}_{cm}$. You need to determine the vector $\vec{r}$ for time $t=0$ . This angular momentum value will remain constant as the system moves upwards. They make this part easy by choosing $m_2=(m_1+m_3)$. The center of mass is on the x-axis, one half the length of an arm of the cross to the right. $\\$ As stated previously, I think you will need this location, as well, in order to compute the moment of inertia of the 3 masses. $\\$ For now though, you needed to compute the location of the center of mass in order to compute the angular momentum caused by the translational motions, (don't forget mass 4). Any missing angular momentum $\\$ (note: these translational motion angular momentums will be less than the initial angular momentum which is conserved) $\\$ will be the rotational angular momentum about its center of mass of the 3 masses.

 

[Eitan Levy]

To get the linear velocity of the center of mass of the 3 coupled masses, you simply need conservation of the linear momentum, using $(m_1+m_2+m_3) \vec{v}_{cm} + m_4 \vec{v}_4=0$. $\\$ And $\vec{v}_{cm}$ will be upward. $\\$ Once you have that, you need to find the location of the center of mass (for the 3 connected masses) in order to compute $L_{1,2,3 \, translational}=\vec{r} \times \vec{p}_{cm}$. You need to determine the vector $\vec{r}$ for time $t=0$ . This angular momentum value will remain constant as the system moves upwards.

That was my intuition, but when I apply it I get a problem. If I look at the cross from the lab frame of reference, I get that that before the collision m₄v₄=m₂v₂. After the collision I get m₄v₄=m₂v₂+(m₁+m₂+m₃)v_CM.
Why did you ignore the momentum caused by the rotational movement of m₂? It doesn't affect the linear momentum because it is created due to rotational movement?

 

[Charles Link]

Use vectors with direction. e.g. $\vec{v}_4$. Do you see that initially the total linear momentum is zero, i.e. $m_1 \vec{v}_1+m_2 \vec{v_2}+m_3 \vec{v}_3+m_4 \vec{v}_4=0$? By conservation of linear momentum that's how I got the result at the top of post 6. (It is at time $t=0^+$, but the $\vec{v}_4$ and $\vec{v}_{cm}$ remain constant after $t=0^+$).

 

[Eitan Levy]

Use vectors with direction. e.g. $\vec{v}_4$. Do you see that initially the total linear momentum is zero, i.e. $m_1 \vec{v}_1+m_2 \vec{v_2}+m_3 \vec{v}_3+m_4 \vec{v}_4=0$? By conservation of linear momentum that's how I got the result at the top of post 6. (It is at time $t=0^+$, but the $\vec{v}_4$ and $\vec{v}_{cm}$ remain constant after $t=0^+$).

I see that, but I can't understand why you ignore the velocity caused by the rotational movement and take only the linear. Do I ignore them because we look at linear momentum? Do they cancel each other out?

I mean, you take only the velocity of the cross and ignore the movement during the rotation, as if the cross isn't rotating at all. Why can you do that?

 

[Charles Link]

Because the masses are balanced,( i.e. $m_1=m_3$ and $m_2=m_4$ ), the cross with 4 masses has zero linear center of mass momentum. And the center of mass is at the center of the cross. $\\$ If the masses were not balanced, the 4 masses would still rotate about the center of mass with zero total linear momentum. $\\$ The total linear momentum is $\vec{p}_{total}= (m_1+m_2 +m_3 +m_4)\vec{v}_{cm}$ which is also $\vec{p}_{total}= m_1 \vec{v}_1+m_2 \vec{v_2}+m_3 \vec{v}_3 + m_4 \vec{v}_4$.$\\$ (I'm pretty sure this is the case=almost certain, but I don't have a simple proof for this at the moment. I think it may be a theorem that gets derived in a Mechanics course). $\\$ Edit: Here is that (simple) proof: Let $\vec{r}_o$ be the center of mass, and $\vec{\omega}$ the angular velocity of the rigid body about the center of mass. $\vec{v_1}=\vec{v}_{cm}+\vec{\omega} \times (\vec{r}_1-\vec{r}_o )$, and similarly for all 4 masses. We need to show the rotation causes zero linear momentum. The total momentum is $m_1 \vec{v}_1+ m_2 \vec{v}_2 + ... =(m_1+m_2 +...) \vec{v}_{cm}+\vec{\omega} \times (m_1 (\vec{r}_1-\vec{r}_o)+m_2 (\vec{r}_2-\vec{r}_o) +...)$. The definition of the center of mass is that this last term in parentheses is zero. $\\$ And meanwhile, no collision takes place. Mass 4 simply comes loose. The total linear momentum, which is zero initially, remains zero. This allows for an immediate calculation of $\vec{v}_{cm}$ for the 3 connected masses after mass 4 comes loose, which I did at the top of post 6. $\\$ Note that for the 3 connected masses, that will be rotating, we still have $(m_1+m_2 +m_3) \vec{v}_{cm}=m_1 \vec{v}_1 +m_2 \vec{v}_2+m_3 \vec{v}_3$. $\\$ And one additional item: The moment of inertia calculation is straightforward because the location of the center of mass of the 3-mass system is a very simple result, and each $r_i^2$ term of the moment of inertia $I=\sum\limits_{i} m_i r_i^2$ can be readily computed by the Pythagorean theorem.

 

[haruspex]

For the first part, you do not need to worry about the detailed construction of the remaining cross. It is just an object of mass m₁+m₂+m₃. You know that the whole system had zero momentum before separation, and that the m₄ part had momentum m₄Lω₀ down, so the rest had that momentum up. The separation does not change either fact.
The linear momentum of an object is always the product of its mass and mass-centre velocity.

 

[Eitan Levy]

Because the masses are balanced,( i.e. $m_1=m_3$ and $m_2=m_4$ ), the cross with 4 masses has zero linear center of mass momentum. And the center of mass is at the center of the cross. $\\$ If the masses were not balanced, the 4 masses would still rotate about the center of mass with zero total linear momentum. $\\$ The total linear momentum is $\vec{p}_{total}= (m_1+m_2 +m_3 +m_4)\vec{v}_{cm}$ which is also $\vec{p}_{total}= m_1 \vec{v}_1+m_2 \vec{v_2}+m_3 \vec{v}_3 + m_4 \vec{v}_4$.$\\$ (I'm pretty sure this is the case=almost certain, but I don't have a simple proof for this at the moment. I think it may be a theorem that gets derived in a Mechanics course). $\\$ Edit: Here is that (simple) proof: Let $\vec{r}_o$ be the center of mass, and $\vec{\omega}$ the angular velocity of the rigid body about the center of mass. $\vec{v_1}=\vec{v}_{cm}+\vec{\omega} \times (\vec{r}_1-\vec{r}_o )$, and similarly for all 4 masses. We need to show the rotation causes zero linear momentum. The total momentum is $m_1 \vec{v}_1+ m_2 \vec{v}_2 + ... =(m_1+m_2 +...) \vec{v}_{cm}+\vec{\omega} \times (m_1 (\vec{r}_1-\vec{r}_o)+m_2 (\vec{r}_2-\vec{r}_o) +...)$. The definition of the center of mass is that this last term in parentheses is zero. $\\$ And meanwhile, no collision takes place. Mass 4 simply comes loose. The total linear momentum, which is zero initially, remains zero. This allows for an immediate calculation of $\vec{v}_{cm}$ for the 3 connected masses after mass 4 comes loose, which I did at the top of post 6. $\\$ Note that for the 3 connected masses, that will be rotating, we still have $(m_1+m_2 +m_3) \vec{v}_{cm}=m_1 \vec{v}_1 +m_2 \vec{v}_2+m_3 \vec{v}_3$. $\\$ And one additional item: The moment of inertia calculation is straightforward because the location of the center of mass of the 3-mass system is a very simple result, and each $r_i^2$ term of the moment of inertia $I=\sum\limits_{i} m_i r_i^2$ can be readily computed by the Pythagorean theorem.

Thanks a ton! Another question, in circular motion v=wr. Does r represent the radius of the circle where the mass spins, or the distance from the center of mass?

 

[Charles Link]

It is spinning about the center of mass. $r$ is the distance from the center of mass which is also the radius of the circle.

 

[Eitan Levy]

It is spinning about the center of mass. $r$ is the distance from the center of mass which is also the radius of the circle.

If I have a pole with a mass of 2m on one side and m on the other they will no be equal, then I need to go to the center of mass to use v=ωr, right?

 

[Charles Link]

Yes, and in this case the center of mass is easy to find. Because they chose $m_2=m_1+m_3$, the x-location of the center of mass for the 3 mass system is $x_{cm}=\frac{L}{2}$. And the y location of the center of mass is at $y_{cm}=0$. $\\$ From this you can compute $\vec{ L}_{1,2,3 \, translational}=\vec{r} \times \vec{p}_{cm}$ for the 3-mass system. You will find that $\vec{L}_{4 \, translational} +\vec{L}_{123 \, translational}$ is less than $\vec{L}_{1234}$ of the initial system. ($\vec{L}$ here is angular momentum in the z-direction). $\\$ By the subscript "translational, it refers to angular momentum computed from the origin of the laboratory frame about which the 4 mass system was initially spinning, and just considering the translational motion of mass 4, and also the translational motion of the center of mass of the system of 3 masses. $\\$ You need to compute $\vec{L}_{4 \, translational}$ and $\vec{L}_{123 \, translational}$, once you have computed $\vec{v}_{cm}$ of the system of 3 masses.

 

[Charles Link]

And note in the equation $\vec{L}_{123 \, translational} =\vec{r} \times \vec{p}_{cm}$ , the $\vec{r}$ here is the initially the distance from the origin to the center of mass of the system of 3 masses, and that $\vec{r}$ is perpendicular to $\vec{p}_{cm}$, so that $\vec{L}_{123 \, translational }$ is readily computed.