- #1
Tanya Sharma
- 1,540
- 135
Homework Statement
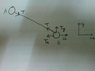
Two particles A and B each of mass m are attached by a light inextensible string of length 2l .The whole system lies on a smooth horizontal table with B initially at a distance l from A.The particle at end B is projected across the table with speed u perpendicular to AB.Find the velocity of ball A just after the jerk ?
Homework Equations
The Attempt at a Solution
The particle at A feels jerk when the string becomes taut.When this happens the angle θ wiill be 30° .
V=velocity of A after the jerk
[itex]u_x[/itex] = x component of velocity of B after the jerk
[itex]u_y[/itex] = y component of velocity of B after the jerk
Using conservation of momentum in y direction we have [itex]u_y[/itex]=vsin30° =v/2
Using conservation of momentum in x direction we have mu = mvcos30°+m[itex]u_x[/itex]
Applying conservation of energy we have
[itex]\frac{1}{2}mu^2 = \frac{1}{2}mv^2+\frac{1}{2}m{u_x}^2+\frac{1}{2}m{u_y}^2[/itex]
Putting the values of [itex]u_x[/itex] and [itex]u_y[/itex] in the above equation and solving
we get v=[itex]\frac{\sqrt{3}}{2}u[/itex]
This is not the correct answer ...Please guide me where am i getting it wrong .