Tanya Sharma
- 1,541
- 135
Homework Statement
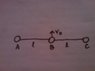
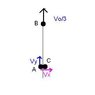
Three identical balls are connected by light inextensible strings with each other as shown and rest over a smooth horizontal table .At the moment t=0,ball B is imparted a velocity.Calculate the velocity of A when it collides with ball C.
Homework Equations
The Attempt at a Solution
Since no external force acts on the system,the CM will continue to move at v_0.
Initially CM is present at ball B.It will continue to move upwards with the same velocity.Momentum of the system remains conserved at all times.
After that I am unable to proceed?