SUMMARY
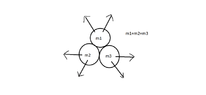
The discussion centers on the conservation of momentum in a system of particles, specifically addressing how momentum is conserved in a closed n-body system as per Newton's laws. It is established that while momentum is conserved for the entire system, it is not necessarily conserved pairwise during interactions between particles. The mathematical proof involves summing the momenta of the particles before and after collisions, demonstrating that the total momentum remains constant when external forces are absent. The conversation also clarifies that Newton's third law applies to each interaction, ensuring that internal forces cancel out, leading to overall momentum conservation.
PREREQUISITES
- Understanding of Newton's laws, particularly Newton's second and third laws.
- Familiarity with vector quantities and their properties.
- Basic knowledge of calculus, specifically integration for impulse-momentum relationships.
- Concept of closed systems in physics.
NEXT STEPS
- Study the mathematical proof of momentum conservation in n-body systems.
- Explore the implications of Newton's laws in multi-particle interactions.
- Learn about the impulse-momentum theorem and its applications in physics.
- Investigate real-world examples of momentum conservation in collisions.
USEFUL FOR
Physics students, educators, and professionals interested in classical mechanics, particularly those focusing on dynamics and the behavior of multi-body systems.