Delta2
Homework Helper
- 6,002
- 2,628
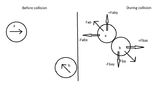
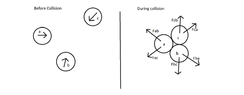
I am not sure what you asking. Deep down we can't be sure about anything but whenever we do experiments in the lab, either microscopic or macroscopic experiments we have found that conservation of momentum holds.mark2142 said:How can you be so sure that these things work in the same way at microscopic level as it works at macroscopic level?
These principles are found out by experimenting with balls and stuffs. Is it because we don't see bodies move on their own? ( For that we need to apply force?)
I hope you understand me.