Construct a low-pass filter and measure the gain

[theuniverse]

Homework Statement

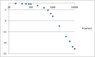
Construct a low-pass filter and measure the gain (Vin/Vout) for a range of frequencies 20 Hz to 10 kHz using an oscilloscope. Plot your data along with the theoretical curve. Use a semi-log graph. What is the half power point for this filter? Does it match the theoretical value based on the components used? (R = 2200 ohm, C = 0.12uF)

The Attempt at a Solution

I plotted the graph and it looks like the one I attached. But I am not too sure what the "half power point" is, or where to find it on my graph. Also how can I calculate a theoretical value for the half power point using my R and C?

Thanks!

PS. Sorry for not having labels on the graph, it's just a rough copy... Ratio of Vin/Vout is on the y-axis and frequency is on the x-axis.

 

[gneill]

Make the x-axis (frequency) a log scale (the problem did ask for a semi-log graph). For more insight, plot the power ratio in dB on the y-axis. That's 20*log(Vo/Vin).

The half power point is where the power available to the load on the output side of the filter is 1/2 the power available at the input. Suppose your load was purely resistive (i.e. there was a very large valued resistor connected across the output of the filter). What would be the power developed by that resistor in terms of the output voltage Vo?

To produce a theoretical curve or find any theoretical values for your filter, you're going to have to derive the expression for |Vo/Vin|. Think impedance.

FYI, the half-power frequency is also called the filter's cutoff frequency, or its -3dB frequency, or its bandwidth.

 

[theuniverse]

Well I know that |Vout/Vin| = Xc/sqrt(R^2+Xc^2) where Xc= 1/(2pi*f*C)
would calculating that with all my frequencies give me the theoretical curve?

Also is the half power point always -3dB? Which would be on my graph ~900Hz?

 

[gneill]

Well I know that |Vout/Vin| = Xc/sqrt(R^2+Xc^2) where Xc= 1/(2pi*f*C)
would calculating that with all my frequencies give me the theoretical curve?

It should.

Also is the half power point always -3dB? Which would be on my graph ~900Hz?

Power varies as the square of the voltage. So when you plot 20*log(x) you're also plotting 10*log(x²). In this case x is your voltage ratio. If the ratio x² is 1/2, then 10*log(1/2) = ?

Also, you might want to invoke a few more grid lines for your frequency axis, the log scale can make it tricky to estimate a frequency with any accuracy. I think you'll find that your -3dB frequency is a tad lower than your 900Hz estimate.

 

[theuniverse]

10*log(1/2) = -3.01 but I found the explanation a little bit confusing at this point "when you plot 20*log(x) you're also plotting 10*log(x2)".

I also plotted my theoretical curve using the formula from my previous post. At -3dB the frequency is close to the experimental values (I'll change the grid and find a more accurate result later on), does it look right?

Also, is the half power point actually measured in Hz (ie. frequency)? so that if I am being asked to find the hpp for a similar curve all I have to do is look for the -3dB (log graph) and its associated frequency?

 

[gneill]

10*log(1/2) = -3.01 but I found the explanation a little bit confusing at this point "when you plot 20*log(x) you're also plotting 10*log(x2)".

I also plotted my theoretical curve using the formula from my previous post. At -3dB the frequency is close to the experimental values (I'll change the grid and find a more accurate result later on), does it look right?

Also, is the half power point actually measured in Hz (ie. frequency)? so that if I am being asked to find the hpp for a similar curve all I have to do is look for the -3dB (log graph) and its associated frequency?

log(b^a) = b*log(a), so 20*log(x) = 10*log(x²).

10*log(x) is the basis of the dB, decibel. The "deci" means 10. 10 bels cover an order of magnitude (power of 10).

The half power point coincides with a certain frequency for a given filter. Yes, you can find it by looking at the power ratio graph (20*log() graph). Just be careful of the frequency axis; sometimes the angular frequency (ω) used.

 

[theuniverse]

I understand it now! Thank you so much gneill!