Continuity of the Bezier Curve, Question

[mymachine]

Hi everyone,

I would like to ask about the continuity of the cubic Bezier curve.

There are two cubic Bezier curves, A and B, shown as below two images:

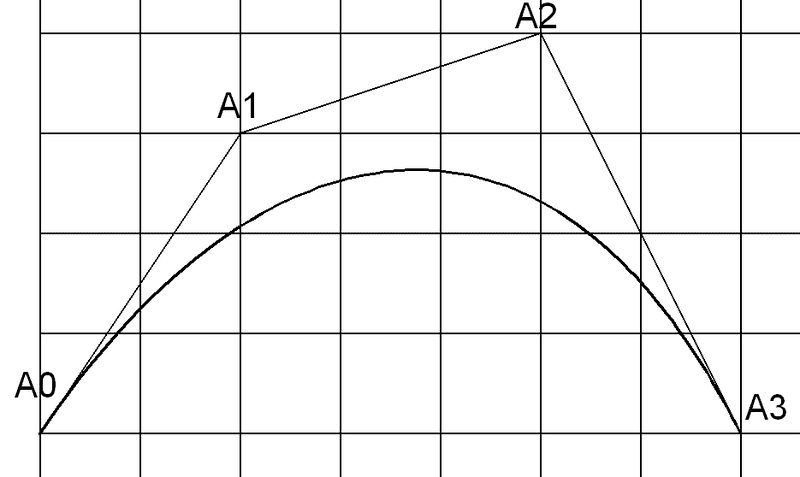
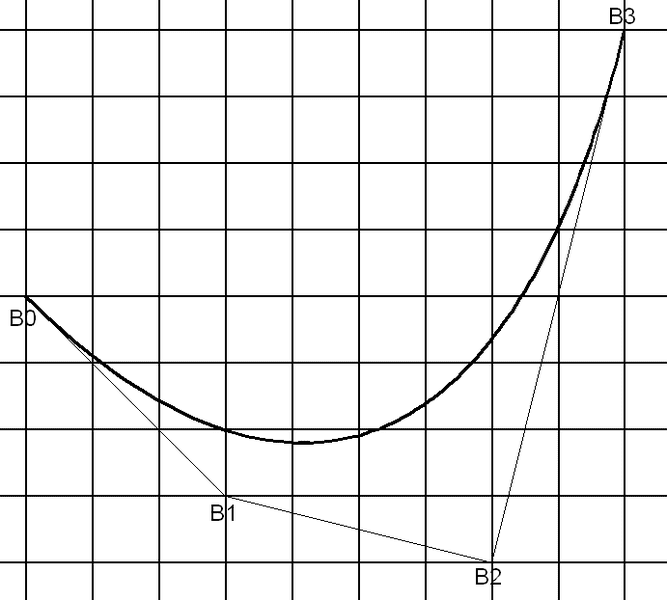
The coordinates of the A curve are:

A0 = (x0,y0) = (0,0)
A1 = (x1,y1) = (2,3)
A2 = (x2,Y2) = (5,4)
A3 = (x3,y3) = (7,0)

The coordinates of the B curve are:

B0 = (x0,y0) = (0,4)
B1 = (x1,y1) = (3,1)
B2 = (x2,y2) = (7,0)
B3 = (x3,y3) = (9,8)

If I join these two curves together by connecting the point A3 and B0, it looks such as below image:

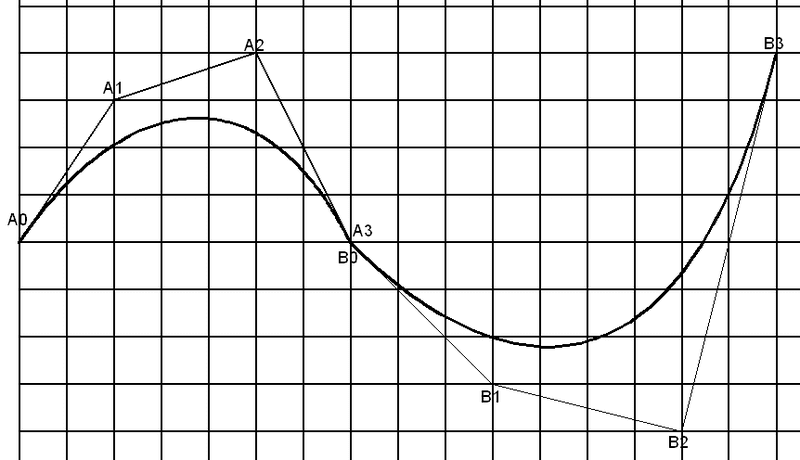
However, the curve doesn't looks smooth at point A3 = B0.

The question is, what is the equation of the Bezier curve start from
point A0 > A1 > A2 > A3=B0 > B1 > B2 > B3
where the endpoint is A0, A3 = B0, and B3
and so that the curve is continue and looks smooth?

Also, does this A+B curve is 7th degree of the Bernstein polynomial?

Thank you

 

[mymachine]

Is it possible if

A2, A3 = B2, and B1

are not colinear

and

A3 = B2

is not the midpoint of A2 and B1?

 

[dodo]

Hi, mymachine,
yes (more or less): the points A2, A3 = B0, and B1 should be collinear. This is because the curve "A" is tangent at A3 to the straight segment A2-A3, and the curve "B" is tangent at B0 to the segment B0-B1. If these two slopes on the curves are to be the same, the segments A2-A3 and B0-B1 must have the same slope too. And since A3=B0, this puts these points on the same straight line.

The two segments A2-A3 and B0-B1 do not need to have the same length (that is, A3 = B0 does not need to be a midpoint of A2-B1).

Your last question, I couldn't understand. The Bernstein polynomials that constitute both the "A" and "B" curves are 3rd-degree polynomials (which is why these are called "cubic" Béziers).

(Just as a side comment, mathematicians use the word "continuity" to refer to the fact that, in your example, A3 = B0; that is, that you didn't need to lift the "pencil" to continue drawing, that the curve does not have a "hole" because of A3 and B0 not coinciding.) Your curve, as described, is continuous; it's just not smooth.

Hope this helps!