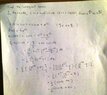Contour integral (please check my solution)
- Context: MHB
- Thread starter aruwin
- Start date
-
- Tags
- Contour integral Integral
Click For Summary
SUMMARY
The discussion focuses on evaluating a contour integral, specifically addressing the path defined by the points from \( e^{-i\pi/2} \) to \( e^{i\pi/2} \) on the unit circle. The user confirms that the contour \( C \) starts at \( -i \) and ends at \( i \), which is crucial for understanding the limits of integration from \(-\pi/2\) to \(\pi/2\). The simplification of the integral is also highlighted by noting that \( \sin\pi = 0 \), which plays a significant role in the evaluation process.
PREREQUISITES- Understanding of complex analysis and contour integration
- Familiarity with the unit circle in the complex plane
- Knowledge of trigonometric identities, specifically \( \sin \) functions
- Basic skills in evaluating integrals in complex variables
- Study the properties of contour integrals in complex analysis
- Learn about the residue theorem and its applications
- Explore the implications of parametrizing paths in the complex plane
- Investigate the significance of singularities in contour integration
Students and professionals in mathematics, particularly those studying complex analysis, as well as anyone involved in evaluating integrals in the context of complex variables.
Similar threads
- · Replies 2 ·
- · Replies 14 ·
- · Replies 7 ·
- · Replies 4 ·
Undergrad
Fourier coefficients of convolution
- · Replies 1 ·
Graduate
Complex Analysis: Contour Integral
- · Replies 2 ·
- · Replies 27 ·
- · Replies 4 ·
- · Replies 6 ·
- · Replies 2 ·