Xyius
- 501
- 4
I only really need help evaluating the contour integral. I added more detail for completeness.
1. Homework Statement
A particle of mass ##m## is constrained to move on the ##x## axis subject to the following potential.
V(x)=a \sec^2\left( \frac{x}{l} \right)
Find the action angle variables ##(\phi,J)##
J=\frac{1}{2\pi}\oint p dq
So I really only need help with the evaluation of the contour integral for J. My background in complex analysis is limited and I believe I must use the residue theorem. I will walk you through what I have.
So first find the lagrangian
##L=T-V=\frac{1}{2}m\dot{x}^2-a\sec^2\left( \frac{x}{l} \right)##
Then find the Hamiltonian using the energy function definition and writing everything in terms of momentum.
##H=\frac{p^2}{2m}+a\sec^2\left( \frac{x}{l} \right)##
Next, use the Hamilton-Jacobi equation to find the generating function (I won't go through this as it is not the focus of my question). From here You can find that ##p=\sqrt{2m(X_0-a\sec^2\left( \frac{x}{l} \right))}## where ##X_0## is the space canonical transformation (acting as a constant for the purposes of the integral next).
So using the equation in section 2 from above, I have the following.
J=\frac{\sqrt{2m}}{2\pi}\oint \sqrt{X_0-a\sec^2\left( \frac{x}{l} \right)}dx
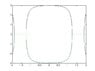
And this is where I am stuck. I believe I need to use the residue theorem, but again my background in complex analysis is limited. So one thing I notice is that because the secant squared is inside the square root, it cannot go to infinity, otherwise the square root becomes complex. ##p## will equal zero when ##x=l \arccos{\sqrt{\frac{a}{x}}}##. So if I plot ##p## I can sort of see it's motion but I am not sure. The curve starts on the Y (or p) axis and then dips down and touches the x axis, then it goes imaginary is is periodic from here. I Believe the path in phase space is such that this dip is mirrored about the y-axis and forms an upside-down parabolic looking shape. From this I can clearly see a closed loop path. Two curves segments making the parabolic-looking shape, and a straight segment connection the two when p=0.
If anyone can offer any help I would appreciate it!
1. Homework Statement
A particle of mass ##m## is constrained to move on the ##x## axis subject to the following potential.
V(x)=a \sec^2\left( \frac{x}{l} \right)
Find the action angle variables ##(\phi,J)##
Homework Equations
J=\frac{1}{2\pi}\oint p dq
The Attempt at a Solution
So I really only need help with the evaluation of the contour integral for J. My background in complex analysis is limited and I believe I must use the residue theorem. I will walk you through what I have.
So first find the lagrangian
##L=T-V=\frac{1}{2}m\dot{x}^2-a\sec^2\left( \frac{x}{l} \right)##
Then find the Hamiltonian using the energy function definition and writing everything in terms of momentum.
##H=\frac{p^2}{2m}+a\sec^2\left( \frac{x}{l} \right)##
Next, use the Hamilton-Jacobi equation to find the generating function (I won't go through this as it is not the focus of my question). From here You can find that ##p=\sqrt{2m(X_0-a\sec^2\left( \frac{x}{l} \right))}## where ##X_0## is the space canonical transformation (acting as a constant for the purposes of the integral next).
So using the equation in section 2 from above, I have the following.
J=\frac{\sqrt{2m}}{2\pi}\oint \sqrt{X_0-a\sec^2\left( \frac{x}{l} \right)}dx
And this is where I am stuck. I believe I need to use the residue theorem, but again my background in complex analysis is limited. So one thing I notice is that because the secant squared is inside the square root, it cannot go to infinity, otherwise the square root becomes complex. ##p## will equal zero when ##x=l \arccos{\sqrt{\frac{a}{x}}}##. So if I plot ##p## I can sort of see it's motion but I am not sure. The curve starts on the Y (or p) axis and then dips down and touches the x axis, then it goes imaginary is is periodic from here. I Believe the path in phase space is such that this dip is mirrored about the y-axis and forms an upside-down parabolic looking shape. From this I can clearly see a closed loop path. Two curves segments making the parabolic-looking shape, and a straight segment connection the two when p=0.
If anyone can offer any help I would appreciate it!
Last edited: