Correspondence Theorem for Groups .... Another Question ....

[Math Amateur]

I am reading the book: "Advanced Modern Algebra" (Second Edition) by Joseph J. Rotman ...

I am currently focused on Chapter 1: Groups I ...

I need help with an aspect of the proof of Proposition 1.82 (Correspondence Theorem) ...

Proposition 1.82 reads as follows:

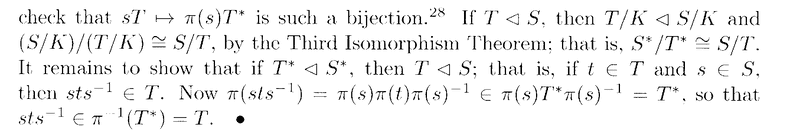
In the above proof by Rotman we read the following:

" ... ... To see that $\Phi$ is surjective, let $U$ be a subgroup of $G/K$. Now $\pi^{-1} (U)$ is a subgroup of $G$ containing $K = \pi^{-1} ( \{ 1 \} )$, and $\pi ( \pi^{-1} (U) ) = U$ ... ... "My questions on the above are as follows:
Question 1

How/why is $\pi^{-1} (U)$ is a subgroup of $G$ containing $K$? And further, how does $\pi^{-1} (U) = \pi^{-1} ( \{ 1 \} )$ ... ... ?
Question 2

How/why exactly do we get $\pi ( \pi^{-1} (U) ) = U$? Further, how does this demonstrate that $\Phi$ is surjective?
Help will be much appreciated ...

Peter

 

[member 587159]

Hi Peter

Question 1:

The preimage of a subgroup of the codomain is always a subgroup of the domain. Try to prove this using the characterisation of subgroups

(i.e., show that $\pi^{-1}(U) \neq \emptyset$ and $a,b \in \pi^{-1}(U) \implies ab^{-1} \in \pi^{-1}(U)$)

$K \subseteq \pi^{-1}(U)$ because $K = \pi^{-1}(\{1\}) = \pi^{-1}(\{e_{G/K}\})$

Question 2:

Furthermore, for any surjective function:

$\pi(\pi^{-1}(U)) = U$.

Try to prove this (set theory question, has nothing to do with groups)

This shows that $\Phi$ is surjective, because you took an arbitrary $U$ subgroup of $G/K$ and then show that $\Phi(\pi^{-1}(U)) = \pi^{-1}(U)/K =\pi(\pi^{-1}(U)) = U$.

Note that it is important here that $\pi^{-1}(U)$ contains $K$, otherwise the quotient is not well defined.

 

[Math Amateur]

Thanks Math_QED ... appreciate your help and support...

Just now reflecting on what you have written ...

Peter

 

[Math Amateur]

Hi Math_QED ...

Taking up your suggestion ...We have that $U$ is a subgroup of $G/K$ ...

Want to show that $\pi^{-1} (U) \neq \emptyset$ and that $a,b \in \pi^{-1} (U) \Longrightarrow ab^{-1} \in \pi^{-1} (U)$Now ...

$\pi( 1_G ) = 1_{ G/K } \Longrightarrow \pi^{-1} ( 1_{ G/K } ) = 1_G$

$\Longrightarrow \pi^{-1} (U) \neq \emptyset$Now ...

... let $a, b \in \pi^{-1} (U)$

$\Longrightarrow \pi(a), \pi(b) \in U$

$\Longrightarrow \pi(a), [ \pi(b) ]^{-1} \in U$ since $U$ is a subgroup ...

$\Longrightarrow \pi(a), \pi( b^{-1} ) \in U$ since $\pi$ is a homomorphism ...

$\Longrightarrow \pi(a) \pi( b^{-1} ) \in U$ since $U$ is a subgroup ...

$\Longrightarrow \pi( a b^{-1} ) \in U$ since $\pi$ is a homomorphism ...

$\Longrightarrow a b^{-1} \in \pi^{-1} (U)$ ...

Therefore $\pi^{-1} (U)$ is a subgroup of $G$ ...Is that correct ...?

Peter

 

[fresh_42]

Is that correct ...?

Yes, it is.

 

[member 587159]

Hi Math_QED ...

$\pi( 1_G ) = 1_{ G/K } \Longrightarrow \pi^{-1} ( 1_{ G/K } ) = 1_G$

$\Longrightarrow \pi^{-1} (U) \neq \emptyset$Is that correct ...?

Peter

The idea is correct, but the line

$\pi( 1_G ) = 1_{ G/K } \Longrightarrow \pi^{-1} ( 1_{ G/K } ) = 1_G$

doesn't make sense. The preimage is a set, and can't be equal to something that isn't a set. Even if you would have written $\{1_G\}$, it wouldn't be correct though.

Notice that $\pi^{-1}(1_{G/K})$ is shorthand notation for $\pi^{-1}(\{1_{G/K}\})$. We are not talking about inverse functions here.

You should rather write $\pi(1_G) = 1_{G/K} \in U$, which means that $1_G \in \pi^{-1}(U)$. Can you explain me why $1_{G/K} \in U$? This is essential here.

The rest is correct.