- 2,453
- 442
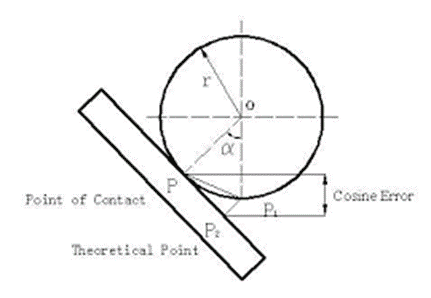
Cosine error of a measured point on the surface is not a simple value, but a vector. If the ball contacts the part surface at a point located a distance from the theoretical or nominal point then the angle between the probe and the normal vector gets larger, P1 P2 will increase. We have cosine error. This error occurs when the part surface varies compared to the CAD nominal. If the angle between the probe actual touch point P and the normal vector P2 gets larger, P1 P2 will increase.
Help..If I have a 5 mm ball tip stylus and can only vector in to the surface at 7.5° how much cosine error will I have?
Help..If I have a 5 mm ball tip stylus and can only vector in to the surface at 7.5° how much cosine error will I have?