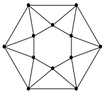
Counting Color Combinations in 12 Triangles
- Context: MHB
- Thread starter maxkor
- Start date
Click For Summary
SUMMARY
The discussion focuses on counting the valid color combinations of 12 triangles, where each triangle's sides can be colored red, green, or blue. The total number of possible colorings is $3^{24}$, but the requirement is that each triangle must have one edge of each color. This constraint significantly reduces the number of valid combinations, leading to a specific combinatorial solution that adheres to the given conditions.
PREREQUISITES- Understanding of combinatorial mathematics
- Familiarity with the concept of permutations and combinations
- Knowledge of basic graph theory
- Experience with mathematical notation and expressions
- Research combinatorial counting techniques in graph theory
- Learn about the principle of inclusion-exclusion in combinatorics
- Explore the application of generating functions for counting colorings
- Study the concept of symmetry in geometric arrangements
Mathematicians, educators, students in combinatorial mathematics, and anyone interested in advanced counting problems and geometric coloring challenges.
Similar threads
High School
Is Each Stage of Pascal's Triangle Special?
- · Replies 11 ·
- · Replies 4 ·
- · Replies 4 ·
- · Replies 1 ·
- · Replies 2 ·
Undergrad
Integer Cevians - Equilateral Triangles
- · Replies 2 ·
- · Replies 3 ·
Undergrad
On Mixing Colors of Light
- · Replies 207 ·
High School
Counting intersections of lines in a triangle
- · Replies 30 ·
- · Replies 40 ·