happyparticle
- 490
- 24
- Homework Statement
- I have to determine the periods of the normal modes.
I have 2 mass ##m_1 = m_2##, l = 1.2m and if I hold vertically one of the mass the period of the other mass is 1.5s.
- Relevant Equations
- F = ma
##m\ddot x = -\frac{mgx_1}{l} -k(x_1 - x_2)##
##m\ddot x_2 = -\frac{mgx_2}{l} +k(x_1 - x_2)##
Hi,
I know there's are 2 normal modes because the system has 2 mass. I did the Newton's law for both mass.
##m\ddot x_1 = -\frac{mgx_1}{l} -k(x_1 - x_2)## (1)
##m\ddot x_2 = -\frac{mgx_2}{l} +k(x_1 - x_2)## (2)
In the pendulum mode ##x_1 = x_2## and in the breathing mode ##x_1 = -x_2##
I get the pendulum and breathing mode by adding equation 1 and 2 and subtracting 1 and 2 then I replace ##x_1-x_2## by q2 and ##x_1+x_2## by q1.
Finally I have ##\omega_p = \sqrt{\frac{g}{l}}## and ##\omega_b = \sqrt{\frac{g}{l} + \frac{2k}{m}}##
It's quite easy to get the period for ##\omega_p##. However, I'm not sure how to find the period for ##\omega_b##, since I don't have k and m.
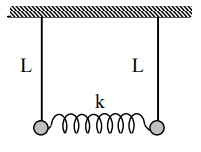
I know there's are 2 normal modes because the system has 2 mass. I did the Newton's law for both mass.
##m\ddot x_1 = -\frac{mgx_1}{l} -k(x_1 - x_2)## (1)
##m\ddot x_2 = -\frac{mgx_2}{l} +k(x_1 - x_2)## (2)
In the pendulum mode ##x_1 = x_2## and in the breathing mode ##x_1 = -x_2##
I get the pendulum and breathing mode by adding equation 1 and 2 and subtracting 1 and 2 then I replace ##x_1-x_2## by q2 and ##x_1+x_2## by q1.
Finally I have ##\omega_p = \sqrt{\frac{g}{l}}## and ##\omega_b = \sqrt{\frac{g}{l} + \frac{2k}{m}}##
It's quite easy to get the period for ##\omega_p##. However, I'm not sure how to find the period for ##\omega_b##, since I don't have k and m.
Last edited by a moderator: