thecommexokid
- 68
- 2
I am reading some of "Planck 2013 results. XXII. Constraints on inflation."
The paper is full of values for various inflationary parameters under various models, with their confidence intervals. For instance, in Table 5 on page 13, the authors report that — for a model including both running of the scalar spectral index and running-of-the-running, and considering Planck+WMAP+BAO data — the best values for the running and running-of-the-running are
\frac{dn_s}{d\ln k}=0.000^{+0.016}_{-0.013}
and
\frac{d^2n_s}{d\ln k^2}=0.017^{+0.016}_{-0.014},
where the ±'s indicate 1σ confidence intervals.
But the individual confidence levels do not tell nearly the whole story, as we see in Figure 3 on page 14, which shows the exact boundaries of the joint 1σ and 2σ confidence interval:
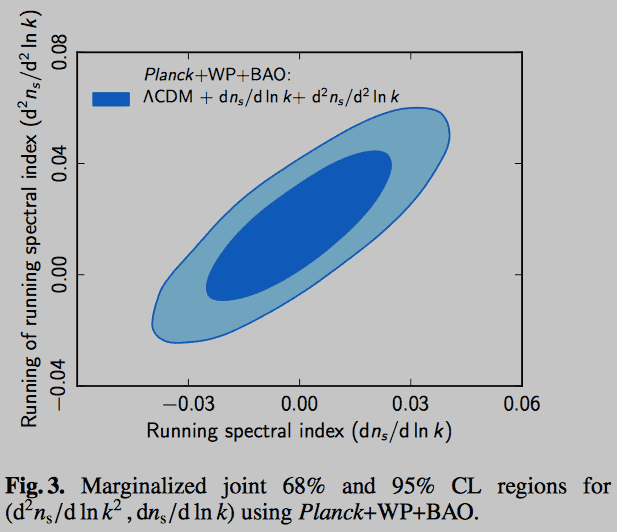
We see in this figure that the running and the running-of-the-running are quite highly correlated, so that you would be quite misled about the joint probabilities if you only had the individual confidence levels from Table 5 without the figure alongside.
Now the numbers I myself am actually interested in are the scalar spectral index ns, which the authors of the Planck paper report in Table 4 (Planck+WMAP+BAO):
n_s = 0.9643\pm 0.0059
and the scalar amplitude As, which they report in Table 3 (Planck+WMAP):
\ln(10^{10}A_s) = 3.089^{+0.024}_{-0.027};
again, the ±'s signify 68% confidence intervals.
What I am doing is to run various simulations with different initial parameters and compute the values of the scalar amplitude and spectral index they predict. I'd like to be able to make some statement about the likelihood of the prediction by comparing to the observed values given in the Planck paper.
Unfortunately, the Planck paper does not contain a plot for scalar amplitude vs. spectral index akin to the one I included above for the running-of-running vs. running. But I imagine that the uncertainties in As and ns are likewise quite correlated, and that simply treating As and ns as independent, skew-normally-distributed parameters is a poor approach.
Are there other Planck papers, or publicly available Planck data somewhere (or for that matter other sections of "XXII" — I freely admit I haven't read the whole thing), that would give me a sense of the shape of the joint confidence interval for As and ns?
The paper is full of values for various inflationary parameters under various models, with their confidence intervals. For instance, in Table 5 on page 13, the authors report that — for a model including both running of the scalar spectral index and running-of-the-running, and considering Planck+WMAP+BAO data — the best values for the running and running-of-the-running are
\frac{dn_s}{d\ln k}=0.000^{+0.016}_{-0.013}
and
\frac{d^2n_s}{d\ln k^2}=0.017^{+0.016}_{-0.014},
where the ±'s indicate 1σ confidence intervals.
But the individual confidence levels do not tell nearly the whole story, as we see in Figure 3 on page 14, which shows the exact boundaries of the joint 1σ and 2σ confidence interval:
We see in this figure that the running and the running-of-the-running are quite highly correlated, so that you would be quite misled about the joint probabilities if you only had the individual confidence levels from Table 5 without the figure alongside.
Now the numbers I myself am actually interested in are the scalar spectral index ns, which the authors of the Planck paper report in Table 4 (Planck+WMAP+BAO):
n_s = 0.9643\pm 0.0059
and the scalar amplitude As, which they report in Table 3 (Planck+WMAP):
\ln(10^{10}A_s) = 3.089^{+0.024}_{-0.027};
again, the ±'s signify 68% confidence intervals.
What I am doing is to run various simulations with different initial parameters and compute the values of the scalar amplitude and spectral index they predict. I'd like to be able to make some statement about the likelihood of the prediction by comparing to the observed values given in the Planck paper.
Unfortunately, the Planck paper does not contain a plot for scalar amplitude vs. spectral index akin to the one I included above for the running-of-running vs. running. But I imagine that the uncertainties in As and ns are likewise quite correlated, and that simply treating As and ns as independent, skew-normally-distributed parameters is a poor approach.
Are there other Planck papers, or publicly available Planck data somewhere (or for that matter other sections of "XXII" — I freely admit I haven't read the whole thing), that would give me a sense of the shape of the joint confidence interval for As and ns?