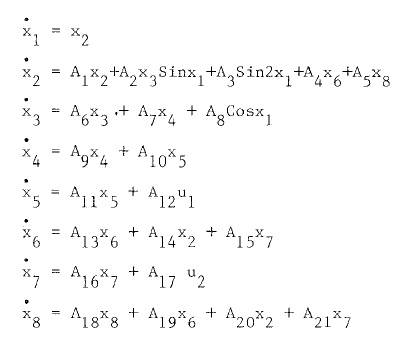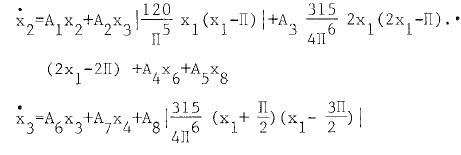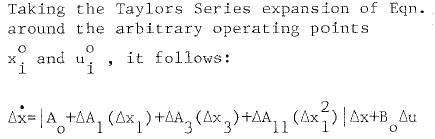SUMMARY
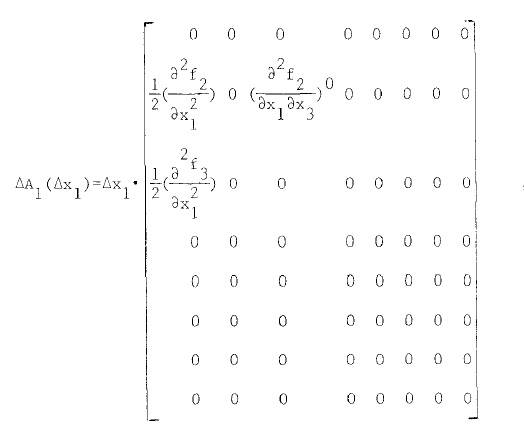
The discussion centers on the confusion surrounding the application of Taylor expansions in the context of state space equations. The original poster seeks clarification on the Taylor expansion of equations X'1 to X'8 and the derivation of coefficients A0, ΔA1, ΔA3, and ΔA11. A key point raised is that the approximations for sine and cosine functions presented are not true Taylor expansions but rather least-squares approximations, which have been identified as inaccurate for certain cases. The community emphasizes the need for correct mathematical formulation and suggests plotting functions to validate approximations.
PREREQUISITES
- Understanding of Taylor series and their applications in mathematics.
- Familiarity with state space equations in control theory.
- Knowledge of least-squares approximation techniques.
- Basic proficiency in plotting functions for visual analysis.
NEXT STEPS
- Study the derivation and application of Taylor series in multivariable calculus.
- Learn about least-squares approximation methods and their mathematical foundations.
- Explore the implications of state space representation in control systems.
- Practice plotting mathematical functions to compare approximations with actual functions.
USEFUL FOR
Mathematicians, control engineers, students in applied mathematics, and anyone involved in numerical methods or approximation techniques will benefit from this discussion.