- #1
long758
- 8
- 5
Here is some background for this post and for future "Curiosity question" posts.
So last year in 10th grade, I took AP Calc AB and AP Physics B, and scored 5s on both, but a particularly high five on the physics, as I truly enjoy doing physics just for the bliss of it. Well this year, I stepped away from physics to do AP Chem, AP Macro, and AP USGov, until January when I learned about the US Physics Olympiad. After taking two F=ma past exams, and scoring within the cutoff for semis, I decided to go for it and do my best. FYI this was without having studied physics at all for 6 months and without even looking at any physics equation sheets (I just used my memory). Since then, I have been self-studying physics and calculus fairly intensely, as I just finished working through the AP Physics C Mechanics syllabus slightly less than a month after starting.
All that to say, over the course of the past month, I have thought up a bunch of physics and math problems, which obviously don't have any published solutions. So I thought I would do a series of sorts with said problems for:
a) the enjoyment of everyone who reads them
b) work checking to see if they are riddled with mistakes or not
c) approach analysis, asking people to give me feedback on how I worked it.
Here is my first problem (hopefully of many). This one, like most of the ones I plan to include in the series I made up:
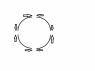
If there is a rope binding a cylindrical object, what is the maximum amount of inward force, as a function of F(tension)? By the way, this is measuring the scalar force, not vector force, because obviously the net force is 0.
I go about the solution by considering simpler regular polygon cross sections, generalizing, and then finding the case of the cylinder by treating its circular cross section as a regular infinity-gon. So there are not many equations needed except for:
the internal angles of a regular polygon = ##180\frac{n-2}{n}##
where n is the number of corners of the polygon.
AND
##\theta = \frac{external angle - 180}{2}##
FYI, there is a fuller solution in the scans, with some musings afterward, but here is the basic approach:
A square, a regular 4-gon, has a rope bound around it. the compressive force can be restricted to the corners only, because its sides are straight. So at each corner, FT acts along the line of its side. Thus, eight FT forces are acting on the square. To find the force inward, I draw a line tangent to the corner and perpendicular to the origin. The inward force from each FT is ##F_T\sin(\theta)##, where theta is ##(external angle - 180) / 2##. It can also easily be shown that ##\theta =\frac{360}{2n}##, where n is the number of corners and 2 is the number of ##\theta##s per corner.
Thus, Total inward force for a square = ##(4 corners)(2 F_Tper corner)(\sin\frac{360}{2*4 corners})##
So for a regular n-gon, Total force = ##F_T n \sin\frac{180}{n}##
So for a circle, and infinity-gon, Total force = ##\displaystyle\lim_{n\rightarrow +\infty} {n\sin(180/n)}##
Numerically, the answer is 2pi, an interesting effect. But what I don't know how to do is to take that limit by non-numerical means. Any help would be appreciated.
Again, if this solution was a bit too concise, or you want to see the diagrams, they are attached.
Thanks!
So last year in 10th grade, I took AP Calc AB and AP Physics B, and scored 5s on both, but a particularly high five on the physics, as I truly enjoy doing physics just for the bliss of it. Well this year, I stepped away from physics to do AP Chem, AP Macro, and AP USGov, until January when I learned about the US Physics Olympiad. After taking two F=ma past exams, and scoring within the cutoff for semis, I decided to go for it and do my best. FYI this was without having studied physics at all for 6 months and without even looking at any physics equation sheets (I just used my memory). Since then, I have been self-studying physics and calculus fairly intensely, as I just finished working through the AP Physics C Mechanics syllabus slightly less than a month after starting.
All that to say, over the course of the past month, I have thought up a bunch of physics and math problems, which obviously don't have any published solutions. So I thought I would do a series of sorts with said problems for:
a) the enjoyment of everyone who reads them
b) work checking to see if they are riddled with mistakes or not
c) approach analysis, asking people to give me feedback on how I worked it.
Here is my first problem (hopefully of many). This one, like most of the ones I plan to include in the series I made up:
Homework Statement
If there is a rope binding a cylindrical object, what is the maximum amount of inward force, as a function of F(tension)? By the way, this is measuring the scalar force, not vector force, because obviously the net force is 0.
Homework Equations
I go about the solution by considering simpler regular polygon cross sections, generalizing, and then finding the case of the cylinder by treating its circular cross section as a regular infinity-gon. So there are not many equations needed except for:
the internal angles of a regular polygon = ##180\frac{n-2}{n}##
where n is the number of corners of the polygon.
AND
##\theta = \frac{external angle - 180}{2}##
The Attempt at a Solution
FYI, there is a fuller solution in the scans, with some musings afterward, but here is the basic approach:
A square, a regular 4-gon, has a rope bound around it. the compressive force can be restricted to the corners only, because its sides are straight. So at each corner, FT acts along the line of its side. Thus, eight FT forces are acting on the square. To find the force inward, I draw a line tangent to the corner and perpendicular to the origin. The inward force from each FT is ##F_T\sin(\theta)##, where theta is ##(external angle - 180) / 2##. It can also easily be shown that ##\theta =\frac{360}{2n}##, where n is the number of corners and 2 is the number of ##\theta##s per corner.
Thus, Total inward force for a square = ##(4 corners)(2 F_Tper corner)(\sin\frac{360}{2*4 corners})##
So for a regular n-gon, Total force = ##F_T n \sin\frac{180}{n}##
So for a circle, and infinity-gon, Total force = ##\displaystyle\lim_{n\rightarrow +\infty} {n\sin(180/n)}##
Numerically, the answer is 2pi, an interesting effect. But what I don't know how to do is to take that limit by non-numerical means. Any help would be appreciated.
Again, if this solution was a bit too concise, or you want to see the diagrams, they are attached.
Thanks!