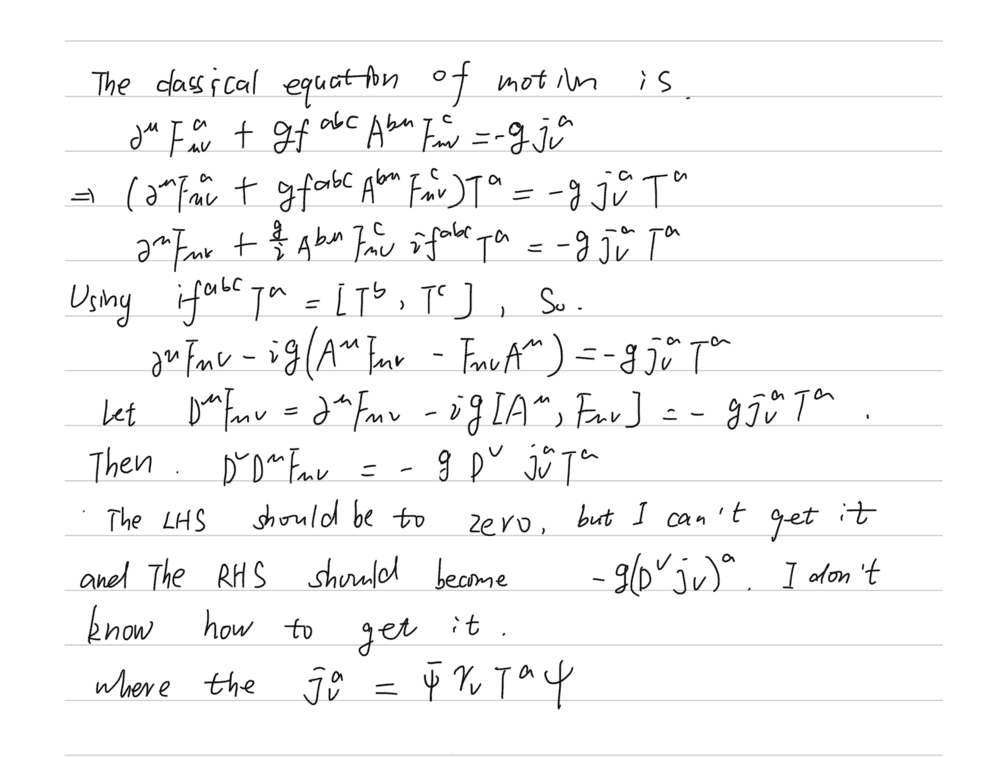SUMMARY
The discussion focuses on implementing current conservation for SU(N) in the adjoint representation, specifically through the equation D^{\mu}F_{\mu\nu} = - j_{\nu}. The solution involves differentiating this equation covariantly and anti-symmetrically, leading to the expression \frac{1}{2}[D^{\mu}, D^{\nu}]F_{\mu\nu} = D^{\nu}j_{\nu}. The covariant derivative in the adjoint representation is defined as D^{\mu}M \equiv \partial^{\mu}M + [A^{\mu}, M], which allows for the conclusion that D^{\nu}j_{\nu} = \frac{1}{2}[F^{\mu\nu}, F_{\mu\nu}] = 0, confirming current conservation.
PREREQUISITES
- Understanding of SU(N) gauge theory
- Familiarity with covariant derivatives in the adjoint representation
- Knowledge of anti-symmetrization in tensor calculus
- Proficiency in matrix-valued fields and their operations
NEXT STEPS
- Study the properties of covariant derivatives in gauge theories
- Explore the implications of current conservation in quantum field theory
- Learn about the adjoint representation in Lie groups
- Investigate the role of field strength tensors in gauge theories
USEFUL FOR
The discussion is beneficial for theoretical physicists, particularly those specializing in gauge theories, quantum field theory researchers, and graduate students studying the mathematical foundations of particle physics.