Current flowing through a resistor in an RRL DC circuit

[greg_rack]

Homework Statement

Determine the current flowing through the circuit(attached below) immediately after having closed the switch.
Values of $V$, $R_1$, $R_2$ and $L$ are given.

Relevant Equations

Ohm's law
Inductance

DISCLAIMER: don't answer in terms of integrals, I haven't covered those yet :)


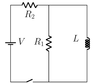
Hi guys, I'm having a few troubles understanding RRL circuits, and have a few questions for you.
A "normal" RL circuit will have a current growing inversely exponentially, starting from 0 and going to $V/R$ as predicted by Ohm's law.

First question: why, intuitively(not algebraically, I know that in order to demonstrate it we must solve a differential equation), is that true?

Then, coming back to our RRL, should we consider the current flowing through $R_1$, immediately after closing the circuit, to be $I=\frac{V}{R_1+R_2}$ with regards to the consideration above for an RL circuit, by which we deduce that the current at $t\approx 0$ flowing in the branch with the inductor, is $I_i\approx 0$?

 

[cnh1995]

>>>>
First question: why, intuitively(not algebraically, I know that in order to demonstrate it we must solve a differential equation), is that true?
<<<<
Intuitively, you can think in terms of energy.
An inductor stores some energy when there is a current flowing through it. This energy cannot jump from zero to a finite amount in zero time. So the current has to start from 0, and increase gradually.

The shape of current vs time graph will depend on the nature of input and other connected elements. This is where algebraic and differential equations come into play.
For an RL circuit excited with a dc voltage source, the resulting differential equation gives an exponentially increasing current.

 

[cnh1995]

Then, coming back to our RRL, should we consider the current flowing through R1, immediately after closing the circuit, to be I=VR1+R2 with regards to the consideration above for an RL circuit, by which we deduce that the current at t≈0 flowing in the branch with the inductor, is Ii≈0?

Yes, I agree with both of your conclusions.

 

[kuruman]

You don't need to solve a differential equation if all you wish to know is the behavior of an uncharged inductor "immediately after" ($t=0$) or "a long time later" ($t\rightarrow\infty$) when a voltage is applied to it. All you have to remember is that an uncharged inductor acts like an open switch "immediately after" and like a short circuit "a long time later". Uncharged capacitors act oppositely: short circuit "immediately after" when they are uncharged and open switch "a long time later" when they are fully charged.

 

[greg_rack]

You don't need to solve a differential equation if all you wish to know is the behavior of an uncharged inductor "immediately after" ($t=0$) or "a long time later" ($t\rightarrow\infty$) when a voltage is applied to it. All you have to remember is that an uncharged inductor acts like an open switch "immediately after" and like a short circuit "a long time later". Uncharged capacitors act oppositely: short circuit "immediately after" when they are uncharged and open switch "a long time later" when they are fully charged.

Great, but why do they act as open switches "immediately after"?

For capacitors(I take advantage of the nice association you have suggested), for instance, we can explain their short-circuiting "immediately after" since, if $q=0$, so will be the voltage $V=qC$ "opposing" that of the EMF.
Is there such an explanation even for inductors?

 

[kuruman]

Great, but why do they act as open switches "immediately after"?

As soon as the inductor is connected to a voltage source, the current through it is zero because the induced emf entirely opposes the current that the source is trying to establish. When zero current goes through a circuit element that circuit element behaves as an open switch. Of course this is instantaneous, i.e. only "immediately after".

You must be familiar with this kind of thinking from kinematics. When you release a weight from rest with air resistance, its velocity "immediately after" is zero and its acceleration is g. A long time later, the weight reaches terminal velocity and its acceleration is zero. When the weight becomes an inductor, velocity becomes current $I$ and acceleration becomes "voltage across" $V_L$. The voltage across is proportional to the time derivative of the current as the acceleration is proportional to the rate of change of velocity. In the former case the constant of proportionality is $-L$ whereas in the latter case it is $1$.

$\dots$ voltage $V=qC$ "opposing" that of the EMF.

You really meant $V=\dfrac{q}{C}$, didn't you?