Current generated by plasma of uneven density in a Magnetic Field

[phantomvommand]

Homework Statement

Please see the attached photo.

Relevant Equations

NA, this is a qualitative question.

I am only asking about part (b)(i) and (b)(ii).

Below is the explanation for (b)(i).

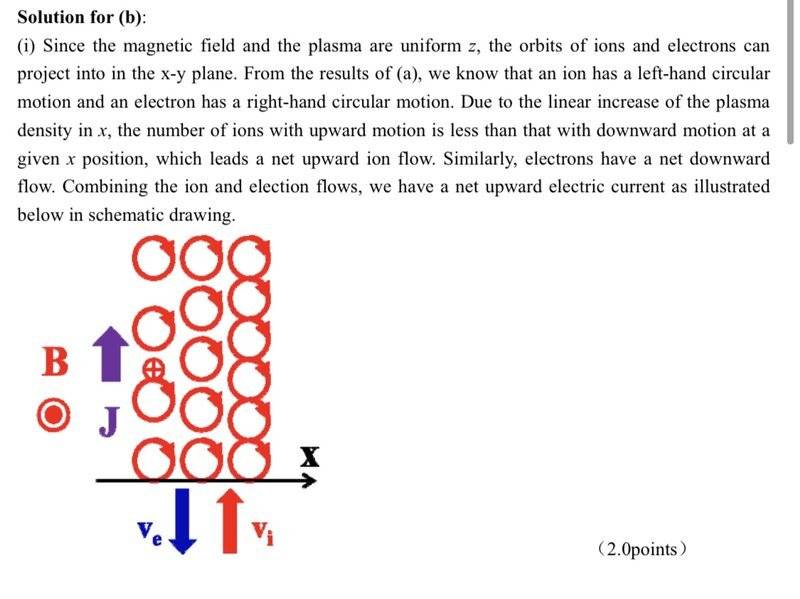
What is going on in the above? I understand up till the 3rd line, about the left/right hand circular motion. What is the "upward motion" the solution mentioned? Is it suggesting that ions are moving upwards, as indicated by the purple arrow J? If so, how is that happening; since pressure is in the X, not Y direction? Furthermore, why would electrons flow in the opposite direction as ions? I think I am unclear about how this "plasma pressure" arises, and thus unaware of its effects.

All help is appreciated.

 

[phantomvommand]

I have since figured this out. I think The question means that there is a velocity parallel to the magnetic field too, hence allowing for an upward/ downward helical movement.

 

[Steve4Physics]

I'm very impressed by the courtesy of the person who wrote the questions. I can't remember seeing 'please' being consistently (or ever!) used in physics questions.