- #1
annamal
- 381
- 33
- Homework Statement
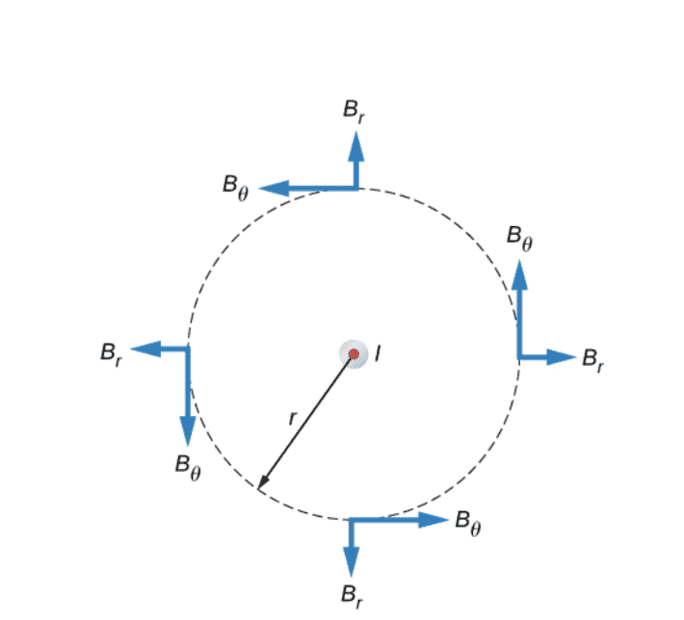
- Use Ampère’s law to calculate the magnetic field due to a steady current I in an infinitely long, thin, straight wire as shown in the image
- Relevant Equations
- ##\oint_{line} B\cdot dl##
Can someone explain how there can be a radial magnetic field? I thought the magnetic field was always tangent to the circle using the right hand rule where you wrap your fingers around the current and point your thumb in the direction of the current.