Saracen Rue
- 150
- 10
Hi everyone,
I am trying to find the definite integral of a function (see attached image) from 0 to infinity using Wolfram alpha. I'm just looking for some verification on if the integral actual is equal to exactly 1, or if there's some rounding errors going on.
Thank you for your time :)
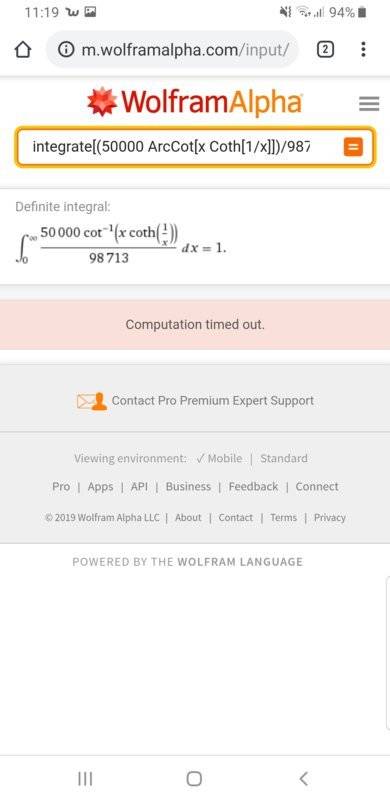
I am trying to find the definite integral of a function (see attached image) from 0 to infinity using Wolfram alpha. I'm just looking for some verification on if the integral actual is equal to exactly 1, or if there's some rounding errors going on.
Thank you for your time :)