Deflection of a cantilever beam with applied tension at the free end

[mrbec]

TL;DR

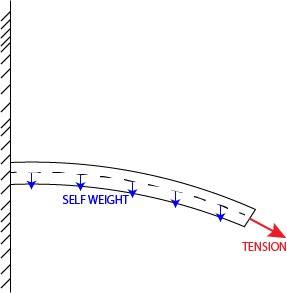
Hello. I would like to know if applying tension to a cantilever beam at the free end affects the deflection it would have otherwise due to only its self weight, and if it does, how to calculate the deflection depending on the tension applied.

Not much to add since the question is fairly simple, but again I'm wondering if applying tension at the free end of a cantilever beam affects the deflection it would have if only itself weight is considered. Intuitively, tension should tend to straighten the beam, and if it does, how to calculate the resulting deflection? Please find below a simple illustration of the problem. Maybe I should also note that tension is always applied and not only after the beam is bent. Sorry for the simplicity of the question and thanks in advance.

 

[Lnewqban]

Welcome!
The original and final directions and magnitude of the tension vector (respect to the stiffness of the beam) are very important.
In other words, how much could the natural deflection of the beam modify the vector tension?

 

[FEAnalyst]

From Roark's Formulas for Stress and Strain: $$y_{max}=\frac{-w}{k^{2}P} \left( \frac{sinhkl \cdot \left( sinhkl-kl \right) }{coshkl} - \left( \left( coshkl-1 \right) - \frac{k^{2}}{2} l^{2}\right) \right)$$ where: $$k=\left( \frac{P}{EI} \right)^{\frac{1}{2}}$$
$w$ - distributed load, $P$ - axial tensile load (there are separate formulas for compressive load case), $l$ - beam length, $E$ - Young’s modulus, $I$ - area moment of inertia.

 

[mrbec]

Welcome!
The original and final directions and magnitude of the tension vector (respect to the stiffness of the beam) are very important.
In other words, how much could the natural deflection of the beam modify the vector tension?

I'm quite confused tbh, but the magnitude of the tension vector is constant, and its final direction depends on the final deflection of the beam since it is along its axis and what i am interested in is how much could the tension vector modify the natural deflection of the beam. Maybe a better way to word my question would be: how does a beam behave when subjected to axial and transverse loads simultaneously? is it possible to use the euler-bernoulli equation to solve the problem? Thanks

From Roark's Formulas for Stress and Strain: $$y_{max}=\frac{-w}{k^{2}P} \left( \frac{sinhkl \cdot \left( sinhkl-kl \right) }{coshkl} - \left( \left( coshkl-1 \right) - \frac{k^{2}}{2} l^{2}\right) \right)$$ where: $$k=\left( \frac{P}{EI} \right)^{\frac{1}{2}}$$
$w$ - distributed load, $P$ - axial tensile load (there are separate formulas for compressive load case), $l$ - beam length, $E$ - Young’s modulus, $I$ - area moment of inertia.

Correct me if I'm wrong but:
-Ymax is the deflection at the free end of the beam,
-w is the weight per length,
-P is the magnitude of the tension applied, and
-l is the length of the beam.
Thanks again.

 

[mrbec]

Correct me if I'm wrong but:
-Ymax is the deflection at the free end of the beam,
-w is the weight per length,
-P is the magnitude of the tension applied, and
-l is the length of the beam.
Thanks again.

I did not see that you added the nomenclature at the end, please ignore what i just said. Anyhow, the equation you provided gives the deflection at the free end of the beam, but is it possible to get the solution for every point along the beam since i want to know the position at which the deflection reaches a certain value? Thanks again.

 

[FEAnalyst]

I did not see that you added the nomenclature at the end, please ignore what i just said. Anyhow, the equation you provided gives the deflection at the free end of the beam, but is it possible to get the solution for every point along the beam since i want to know the position at which the deflection reaches a certain value? Thanks again.

Yes, but I would rather call $w$ force per unit length (N/m).

Actually, the book also gives a formula for the deflection at any given point of the beam (with $x$ coordinate denoting distance from free end): $$y=y_{max}+ \frac{\theta_{max}}{k} sinhkx+LT_{y}$$ $$\theta_{max}=\frac{w}{kP} \cdot \frac{sinhkl-kl}{coshkl}$$ $$LT_{y}=\frac{-w}{Pk^{2}} \cdot (coshkx-1)- \frac{k^{2}}{2} x^{2}$$

 

[mrbec]

Actually, the book also gives a formula for the deflection at any given point of the beam (with $x$ coordinate denoting distance from free end): $$y=y_{max}+ \frac{\theta_{max}}{k} sinhkx+LT_{y}$$ $$\theta_{max}=\frac{w}{kP} \cdot \frac{sinhkl-kl}{coshkl}$$ $$LT_{y}=\frac{-w}{Pk^{2}} \cdot (coshkx-1)- \frac{k^{2}}{2} x^{2}$$

I'll try to work my way with this formula and see where it gets me. Thank you very much.

 

[Dr.D]

From Roark's Formulas for Stress and Strain: $$y_{max}=\frac{-w}{k^{2}P} \left( \frac{sinhkl \cdot \left( sinhkl-kl \right) }{coshkl} - \left( \left( coshkl-1 \right) - \frac{k^{2}}{2} l^{2}\right) \right)$$ where: $$k=\left( \frac{P}{EI} \right)^{\frac{1}{2}}$$
$w$ - distributed load, $P$ - axial tensile load (there are separate formulas for compressive load case), $l$ - beam length, $E$ - Young’s modulus, $I$ - area moment of inertia.

What edition of Roark would that be, please?

 

[FEAnalyst]

What edition of Roark would that be, please?

I’ve found this formula in eighth edition of Roark’s, page 270 (table 8.9. Shear, Moment, Slope, and Deflection Formulas for Beams Under Simultaneous Axial Tension and Transverse Loading).

 

[Dr.D]

Thanks for the specific citation in Roark. That helps.