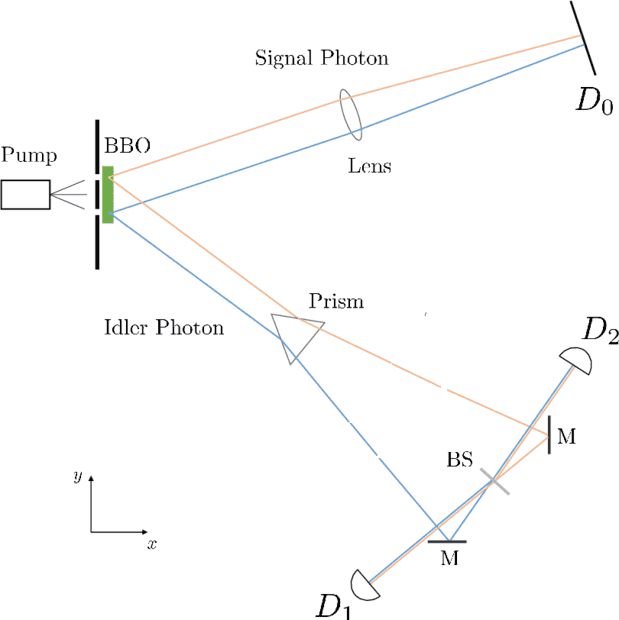
I must however, correct myself concerning the explanation for the no-interference pattern at ##D_0## in the other thread. That was wrong. It's not due to the photons coming from the upper or lower slit being downconverted at different places but due to orthogonality of the two entangled states.
Now in the setup drawn the photons moving in direction of detector ##D_0## (at location ##\vec{x}_1##), defining the "signal photons" are sent through the lens such that all rays in parallel direction are refracted to one point, i.e., there's no which-way information somehow stored in these photons, i.e., you can never say from which slit the original laser photon came and at which spot of the BBO it was down-converted.
In order for the eraser experiment to work, however, the idler photons must be separated depending on the location they came from, and that's what the prism is good for, i.e., for the idler photon, after the prism but before the mirrors and the beam splitter by putting detectors at the two well-separated places you know from which slit the original photon came.
So this situation is described by
$$|\Psi \rangle=\frac{1}{\sqrt{2}} (|\psi_1^{(S)},\psi_1^{(I)} \rangle + |\psi_2^{(S)},\psi_2^{(I)} \rangle).$$
Here the superscripts ##(S)## and ##(I)## refer to the idler photons and the subscripts 1 and 2 the source (slit 1 or slit 2 of the original then downconverted photons). These states are such that
$$\langle \psi_1^{(I)}|\psi_2^{(I)} \rangle=0$$
when the idler photons are registered at places after the prism but before the mirrors and the beam splitter.
Then you get
$$\langle \Psi|\Psi \rangle=\frac{1}{2} (\langle \psi_1^{(S)}|\psi_1^{(S)} \rangle \langle \psi_1^{(I)}|\psi_1^{(I)} \rangle + \langle \psi_2^{(S)}|\psi_2^{(S)} \rangle \langle \psi_2^{(I)}|\psi_2^{(I)} \rangle.$$
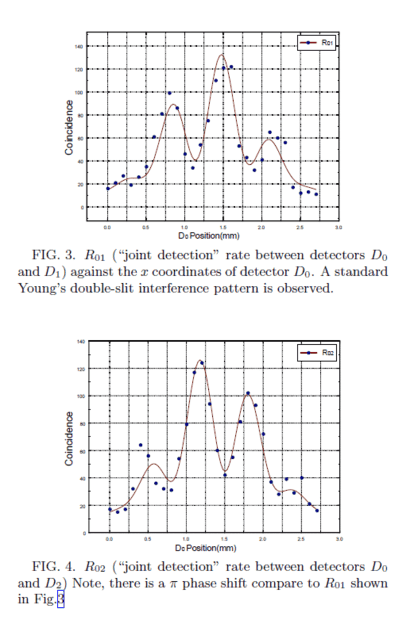
So you get no double-slit interference fringes at ##D_0## but rather an incoherent addition of the single-slit interference patterns for photons coming from either slit 1 or slit 2. These are slightly shifted against each other due to the distance between the sources, and you get a pretty broad pattern. As seen in the original paper (the PRL published version), in the range ##D_0## was placed this is simply a flat line.
Now take the situation after the mirrors and the beam splitter (for simplicity assuming a symmetric beam splitter). Then the idler photon states get modified in the following way (in your simplified experiment depicted in #1)
$$|\psi_1^{(I)} \rangle \rightarrow \frac{1}{\sqrt{2}} (\mathrm{i} \psi_{D_1}^{(I)} - \psi_{D_2}^{(I)})=| \psi_1^{\prime (I)}\rangle$$
and
$$|\psi_2^{(I)} \rangle \rightarrow \frac{1}{\sqrt{2}} (- \psi_{D_1}^{(I)} + \mathrm{i} \psi_{D_2}^{(i)})=\langle \psi_2^{\prime (I)} \rangle,$$
where I took into account the ##\pi/2## phase shift for each reflection either on the mirror or the beam splitter. That's a unitary transformation (assuming ideal, lossless mirrors and beam splitter).
Now we have for the two-photon state (after some simple algebra)
$$|\Psi ' \rangle=\frac{1}{\sqrt{2}} \left ( |\mathrm{i} \psi_1^{(S)}-\psi_2^{(S)},\psi_{D_1}^{(I)} \rangle + |-\psi_1^{(S)} + \mathrm{i} \psi_2^{(S)},\psi_{D_2}^{(I)} \rangle \right).$$
If you take all the photons again you don't get an interference pattern at ##D_0##, and indeed the mirrors and beam splitters only interacted with the idler photon and doesn't affect the signal photon.
Of course, if you now only look at the cases, where ##D_1## registered an idler photon, then you get for the probability to register the signal photon
$$R_{01}=\frac{1}{2} \left [\langle \psi_1^{(S)}|\psi_1^{(S)} \rangle + \langle \psi_2^{(S)}|\psi_2^{(S)} \rangle + \mathrm{i} (\langle \psi_1^{(S)}|\psi_2^{(S)} \rangle-\langle \psi_2^{(S)}|\psi_1^{(S)} \rangle) \right],$$
and if you project to outcomes, when ##D_2## registered an idler photon,
$$R_{02}=\frac{1}{2} \left [\langle \psi_1^{(S)}|\psi_1^{(S)} \rangle - \langle \psi_2^{(S)}|\psi_2^{(S)} \rangle+ \mathrm{i} (\langle \psi_1^{(S)}|\psi_2^{(S)} \rangle-\langle \psi_2^{(S)}|\psi_1^{(S)} \rangle) \right].$$
In both cases you get a two-slit interference pattern due to the interference terms.