cookiemnstr510510
- 162
- 14
Homework Statement
a)recall that electric potential is a scalar quantity. For a circular ring of radius, R', carrying charge, Q, what is the electric potential at a height,y, above the center of the ring?
b)Use your above answer to determine the electric potential at a height,y, above the center of a uniformly charged disk of radius, R.
c)if y>>R, use the binomial expansion (keeping terms up to and including R2/y2 ) to show that the electric potential now resembles that of a point charge
Homework Equations
V=q/(4πε0r)
The Attempt at a Solution
a)V=q/(4πε0r)
dv=dq/(4πε0)
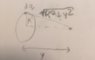
See ring.jpg attached
V=∫dv=∫dq/(4πε0)=[1/(4πε0r)]∫dq=q/4πε0r=q/4πε0(R'2+y2)1/2
b)See disk.jpg attached
V=kq/(R'2+y2)1/2
dV=kdq/(R'2+y2)1/2
(dq/Q)=(2πR'dr/πR2)→dq=2QR'dr/R2
The limits on the below integral are from 0→R until stated differently
V=∫dV=∫(k2QR'dr)/[R2(R'2+y2)1/2]=(kQ/R2)∫2R'dr/(R'2+y2)1/2
Usub:
U=R'2+y2
dU=2R'dr
dr=dU/2R'
New Limits:
when r=0, U=y2
when r=R, U= R2+y2
after taking integral:
(KQ/R2) [u1/2]evaulated from y2→R2+y2=(KQ/R2)[(R2+y2)-y]
c) This is the part I am confused on... not sure where to start.
I know if y>>R then my above answer turns into
(KQ/R2)[y2-y] but other than that not sure where to go...