greg_rack
Gold Member
- 361
- 79
Hi guys, in the derivation of the Euler equation we apply Newton's 2nd law to a gas flowing through a streamline. To do so, we consider a "box" with sides ##dx## ##dy## and ##dz##:
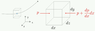 as such;
as such;
Here, with reference to the image, I can't understand where does that '##+dp##' comes from, and hence why the pressure would vary on the right side of the box compared to that acting on the left side.
Here, with reference to the image, I can't understand where does that '##+dp##' comes from, and hence why the pressure would vary on the right side of the box compared to that acting on the left side.