- #1
CGandC
- 326
- 34
Homework Statement
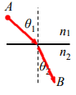
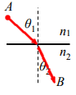
Prove that snell's law ## {n_1}*{sin(\theta_1)} ={n_2}*{sin(\theta_2)} ## is derived from using euler-lagrange equations for the time functionals that describe the light's propagation, As described in the picture below.
Given data:
the light travels in two mediums , one is ## n_1 ## and the other is ## n_2 ##
The speed of the light in these mediums are:
## v_1=\frac{c}{n_1} ## and ## v_2=\frac{c}{n_2} ## respectively
and the angles of incident and refraction are: ## \theta_1 ## and ## \theta_2 ## respectivley
Homework Equations
## \frac{d}{dt} \left ( \frac{\partial L}{\partial \dot q} \right ) - \frac{\partial L}{\partial q}=0 ##
## distance = speed*time## ,## t_0 = 0 ## and the velocity is constant
## Arclength = ds = \sqrt{dx^2+dy^2} ##
The Attempt at a Solution
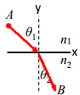
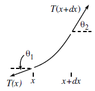
I'll look at medium ## n_1 ## : I'll look at an infinitesimal piece of the arclength of the light:
and using the distance formula
##{v_1*dt}={\sqrt {( x-(x+dx) )^2+( y-(y+dy) )^2} }={\sqrt{( dx) )^2+( dy) )^2}}={\sqrt {1+\frac{dy}{dx}^2} }*dx ##
so: ## t =
\int \frac{ds}{v_1}=\int \frac{\sqrt{dx^2+dy^2}}{v_1}=\int \frac{\sqrt{1+y'^2}}{v_1}dx
##
Using euler lagrange equations, I find that ## y ## is a cyclical coordinate, therefore:
## \frac{d}{dx} \left ( \frac{y'}{v_1*\sqrt {1+(y')^2}} \right )=0 ##
so: ## \frac{y'}{v_1*\sqrt {1+(y')^2}} =const ## and re-arranging:
## \frac{dy}{v_1*\sqrt{dx^2+dy^2}} = const ##
knowing that ( from the pictures) : ## \frac{dy}{\sqrt{dx^2+dy^2}}=\frac{dy}{ds} =cos(\theta_1) ## and that
## v_1=\frac{c}{n_1} ## then I can re-write ## \frac{dy}{v_1*\sqrt{dx^2+dy^2}} = const ## as:
## {n_1}*{cos(\theta_1)}/c = const ##
Using similar methodology with the second medium, I get: ## {n_2}*{cos(\theta_2)}/c = const ##
I notice that there is a conserved quantity from the euler-lagrange equations, therefore:
## {n_1}*{cos(\theta_1)} ={n_2}*{cos(\theta_2)} ##
So here's the problematic point , I got : ## {n_1}*{cos(\theta_1)} ={n_2}*{cos(\theta_2)} ## instead of : ## {n_1}*{sin(\theta_1)} ={n_2}*{sin(\theta_2)} ##
What seems to be the problem? is it my understanding of what I'm doing with the euler-lagrange equation?