- #1
JohnTravolski
- 18
- 0
Moved from a rechnical forum, so homework template missing
I'm really lost on this one.

I'm really not sure how to get started on this. I started it out as a force problem and solved for ax = g*cos(theta). I then integrated that (treating it like a constant) from zero to D to find my initial velocity at the time the block reaches the edge of the cliff. I then used the position function:
y=y0+v0yt+1/2ayt^2
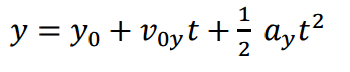
to determine the time it takes to hit the ground, but I don't understand how any of this will help me find the angle φ. I'm really just lost. Can somebody please work this problem so I won't be so confused?
I'm really not sure how to get started on this. I started it out as a force problem and solved for ax = g*cos(theta). I then integrated that (treating it like a constant) from zero to D to find my initial velocity at the time the block reaches the edge of the cliff. I then used the position function:
y=y0+v0yt+1/2ayt^2
to determine the time it takes to hit the ground, but I don't understand how any of this will help me find the angle φ. I'm really just lost. Can somebody please work this problem so I won't be so confused?