Derive error formula for Lambda (25 C)

[lep11]

In physics lab course I measured equivalence conductivity of NaCl in infinite dilution Λ₀ as a function of temperature T.

So I have observations (T, Λ₀) and fitted a line using the least squares method in Ms excel (lol ).
The formula of the line is Λ₀(T)=c₀+c₁T, where c₀ and c₁ are constants.

I am asked to estimate the error of Λ₀(25 C) using the following formula

σ_Λ0(T)=(C₁₁+T(C₁₂+C₂₁)+T²C₂₂),

where C_ij are elements of covariance matrix and T is temperature in centigrades. I have matlab, but don't know the commands and how to calculate.

I am also asked to derive the formula above on paper and honestly I have no idea where to begin.
However, I am given this clue;

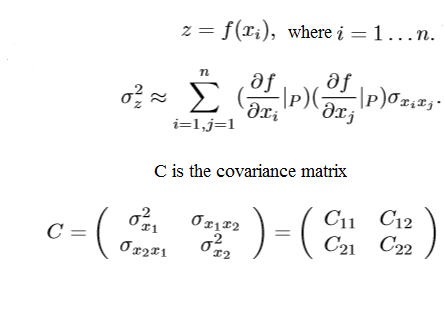
Those partial derivatives confuse me

I will appreciate any help!

 

[BvU]

No responses so far, must be a complicated subject ...

You used excel linest ? Did it give you the whole matrix ?

Reason you need the off-diagonal elements is that the errors in $c_0$ and $c_1$ are correlated: the fitted line goes through the center of gravity of the measurements, which generally is not on the y-axis. 'Wiggling' the line shows that the error in the intercept is partially due to the error in the slope.

Does this thread help you ? Or the references mentioned ?

 

[lep11]

You used excel linest ? Did it give you the whole matrix ?

Yes and yes.

Does this thread help you ? Or the references mentioned ?

Not really, unfortunately.

 

[BvU]

Well, then we have to go through step by step. Partial derivatives pop up when functions are functions of more than one variable. Generally error propagation works with partial derivatives. Errors are supposed to be small and the derivatives give a linear approximation for the propagation.

Show what you have so far and we'll pick it up at σ_Λ0(T)=(C₁₁+T(C₁₂+C₂₁)+T²C₂₂), which I find strange: T shouldn't appear there.

 

[lep11]

Okay, now I think I've figured it out. I have to submit my work due to Monday.

Does this make any sense?
The error of line fitting is function of c₁ and c₂.

Sorry, the picture is a bit blurry and unclear.

The only problem is, how do I get the covariance-variance matrix between c₁ and c₂?

(I know C11 and C22 because excel gave variances, but C12 and C21 are still unknown.)