How do I find the differential equation for this circuit?

[arhzz]

Homework Statement

Find the differential equation

Relevant Equations

-

Hi,

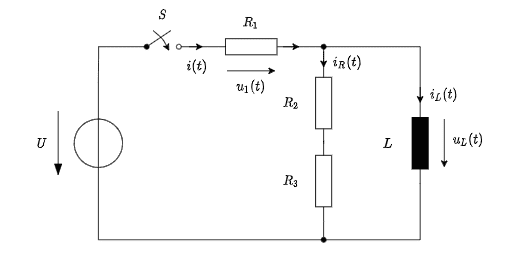
The following circuit is given, where the switch S is closed at time t=0.
a) Set up the general differential equation (DE) for the current i(t) and bring the result into the following form$\frac{di(t)}{dt} +c_1 i(t)=c_0,$ with the constant terms c0 and c1.
Hint: Determine the DE using Kirchoffs laws
b) established ODE.Use here for the exponential approach,i.e. $i_h(t)=ke^{λt}.$
(c) Determine the particular solution of the DE
(d)Determine the constant k
(e) Find out the values when i(t) aproaches 0 and infinity, as well as for $u_L (t)$ Sketch them in a graph

Okay so I'm having problems right at the start. So first I figured that $i(t) = i_R(t) + i_L(t)$ Using the loop law I get; $U = u_1 + u_L(t)$ and I can rewrite that as $i(t)R_1+ L\frac{di_L(t)}{dt}$ now I have rewritten the first equation to look like this; $i_L(t) = i(t) - u_L(t)(R2+R3)$ and now what I have tried is plugging in the first equation in the second one.

$$ U = i(t)R1 + L \frac{d}{dt} (i(t) - u_L(R2+R3) $$ and here is the problem.I get the derivative of di/dt but I'm stuck with this voltage.Usually its a constant term meaning after deriving it simply goes to 0. Now I've tried mixing it up but the same problem persits.I've went ahead and done the rest of the problem,under the assumption that the UL term goes to 0,and the solutions look right ( I get the the right time constant). Can it be that the voltage really goes to 0, if so why? If not what am I doing wrong than?

Thanks for the help!

 

[Delta2]

One obvious mistake I see is that $u_1(t)=i(t)R_1$ please fix that and hold on while I think over this more.

 

[Delta2]

You have confused me with your approach. One equation is for sure from the KCL $$i(t)=i_R(t)+i_L(t)$$.
Write two more equations from applying KVL in any two of the 3 possible loops and express everything in terms of currents, so if you have $u_L$ for example, write it down as $L\frac{di_L}{dt}$.

At the end you will have a system of 3 DEs with 3 unknowns the 3 currents $i(t),i_R(t),i_L(t)$.

 

[arhzz]

You have confused me with your approach. One equation is for sure from the KCL $$i(t)=i_R(t)+i_L(t)$$.
Write two more equations from applying KVL in any two of the 3 possible loops and express everything in terms of currents, so if you have $u_L$ for example, write it down as $L\frac{di_L}{dt}$.

At the end you will have a system of 3 DEs with 3 unknowns the 3 currents $i(t),i_R(t),i_L(t)$.

Why us u1 = i(t)•R1 wrong? Is not the voltage current times resistance? Than for the other equations ; The first one is KCL,but I do not see the other two? I have one KVL and that is U = uL • u1 and I have (at least tried) expressing it in terms of currents (see post #1). Where do I find the third equation?

 

[Delta2]

yes sorry i meant you seem to have $u_1=\frac{i(t)}{R_1}$. The other KVL is $u_L=i_R(t)(R_2+R_3)$.

 

[Delta2]

The three equations are $$i(t)=i_R(t)+i_L(t)$$
$$L\frac{di_L(t)}{dt}=i_R(t)(R_2+R_3)$$
$$U=i(t)R_1+L\frac{di_L(t)}{dt}$$

 

[arhzz]

yes sorry i meant you seem to have $u_1=\frac{i(t)}{R_1}$. The other KVL is $u_L=i_R(t)(R_2+R_3)$.

Oh wait you are right, I will fix that now.I am currently on my phone,I will try the problem again some time tonight,using these 3 new equations. I am pressuming I need to rearrange 2 equations and plug them into one?

 

[Delta2]

The way I did this is first to eliminate $i_R(t)$ from (1) using (2), then solve the DE you get for $i_L(t)$ (it will be an integral of $i(t)$) and then replace $i_L(t)$ in the third and you ll get a DE for i(t).

 

[Delta2]

The way I did it is not so straightforward, it is really a practice of skills in algebra, derivatives and integrals, maybe there is a clever shortcut but I can't think of any at the moment.

 

[arhzz]

The way I did it is not so straightforward, it is really a practice of skills in algebra, derivatives and integrals, maybe there is a clever shortcut but I can't think of any at the moment.

I see I have tried to replicate it,and it will take some time.I will keep trying and if I'm really stuck I will post. Thanks for the help this far ! Hopefully I can solve it :)

 

[Delta2]

Actually I think there is an easier way, the solution for $i_L$ seems to lead to an integral equation which I ve never seen before, so its better to eliminate $i_L$ and $\frac{di_L}{dt}$.
First use (2) and (3) to eliminate $\frac{di_L}{dt}$ and find $i_R(t)$ in terms of $i(t)$ call that equation (4).

Then take the time derivative of (1) and replace $\frac{di_L}{dt}$ in (2), call that equation (5)

In (5) replace $i_R(t)$ with what you get from (4).

 

[arhzz]

Actually I think there is an easier way, the solution for $i_L$ seems to lead to an integral equation which I ve never seen before, so its better to eliminate $i_L$ and $\frac{di_L}{dt}$.
First use (2) and (3) to eliminate $\frac{di_L}{dt}$ and find $i_R(t)$ in terms of $i(t)$ call that equation (4).

Then take the time derivative of (1) and replace $\frac{di_L}{dt}$ in (2), call that equation (5)

In (5) replace $i_R(t)$ with what you get from (4).

Okay I will try this. I have tried the method with the integral and I could not pull it off. As you said I cannot solve the integral equation, not only have I never seen it I have never solved any integral equation. My biggest hope was that I could simply use the fact that current in a inductivity is an integral of the voltage but that did not work out.

I will try this method, I've thought about eliminating iL first since it is the one that is causing the issue. I think I can pull this one off.

 

[berkeman]

I've went ahead and done the rest of the problem,under the assumption that the UL term goes to 0,and the solutions look right ( I get the the right time constant). Can it be that the voltage really goes to 0, if so why?

Yes, $u_L$ goes to zero eventually, because the ideal inductor $L$ is a DC short.

 

[arhzz]

Yes, $u_L$ goes to zero eventually, because the ideal inductor $L$ is a DC short.

Yes but that would be what I would need for the particular solution right ? That is also a question I have been having. When setting up the DE and with setting up I mean the a) part of the problem can I "think ahead" and use the fact what happens with L and C after a long time or right after closing the circuit (so t --> 0)? Or simply stick to Kirchoffs Laws when setting up the DE?

 

[berkeman]

You will use the boundary conditions to find the particular solution. I would use t=0+ and t=infinity to help constrain the DE. Is that what you are asking?

 

[arhzz]

I think that is what I am asking, can you elaborate a bit more on what you mean by constraining the DE? Are you looking what happens with L at 0+ and infinity? And that really was the point of my question, am allowed to constraint the DE, won't that give me a faulty DE?

You will use the boundary conditions to find the particular solution. I would use t=0+ and t=infinity to help constrain the DE. Is that what you are asking?

 

[berkeman]

You are constraining the particular solution of the DE based on the boundary conditions of the problem. If the switch were being opened after a long time instead of being closed, that would give you different boundary conditions and different values of the constants in the particular solution, no?

So yes, since the current through an inductor cannot change instantaneously, the inductor acts like an open circuit at t=0+, and looks like a short circuit at t=infinity. That defines the voltages across those nodes where the inductor is connected for both t=0+ and t=infinity, which should allow you to find the constants for the particular solution.

 

[arhzz]

Ah, I see that was pretty much what I was thinking. Thanks!

You are constraining the particular solution of the DE based on the boundary conditions of the problem. If the switch were being opened after a long time instead of being closed, that would give you different boundary conditions and different values of the constants in the particular solution, no?

So yes, since the current through an inductor cannot change instantaneously, the inductor acts like an open circuit at t=0+, and looks like a short circuit at t=infinity. That defines the voltages across those nodes where the inductor is connected for both t=0+ and t=infinity, which should allow you to find the constants for the particular solution.

 

[Delta2]

I don't think it is correct to put $u_L=0$ while forming the differential equation for $i(t)$.

 

[berkeman]

I don't think it is correct to put $u_L=0$ while forming the differential equation for $i(t)$.

That's a boundary condition to be applied for t=infinity in order to solve for the coefficients, not for use in generating the DE.

 

[arhzz]

I don't think it is correct to put $u_L=0$ while forming the differential equation for $i(t)$.

Got it. I have been trying really hard to replicate your method of getting the equation for i(t) but I think I am making a mistake somewhere. Here is how I tried it;

So we want to use (2) and (3) to eliminate the derivatife of iL. This is how I've tried it

(3) $U - i(t) R_1 = L \frac{di_L(t)}{dt}$ Now plug this for the derivative in equation two and find iR(t)

$i_R(t) = \frac{U-i(t)R_1}{R_2+R_3}$ We call this equation (4) Now here is where I think I got something wrong. "Take the time derivative of (1) and plug that for the derivative of iL" ; Deriving (1)

$$ \frac{di(t)}{dt} - \frac{di_R(t)}{dt} = \frac{di_L(t)}{dt} $$ And now I am assuming I need to plug this into the original (2) equation? That should look like this;

$$ L (\frac{di(t)}{dt} - \frac{di_R(t)}{dt}) = i_R(t) (R2+R3) $$ Now I'm susposed to find iR here call that equation (5);

$$ L (\frac{di(t)}{dt} - \frac{di_R(t)}{dt}) * \frac{1}{R2+R3} = i_R(t) $$ so this should be equation 5

Now if I replace iR in (5) with what I have from 4 ;

$$ L (\frac{di(t)}{dt} - \frac{di_R(t)}{dt}) * \frac{1}{R2+R3} = \frac{U-i(t)R_1}{R_2+R_3} $$

Now the problem is this derivative of iR? Where did I make a mistake?

 

[Delta2]

correct so far (with some minor typos) hold because i am abit busy atm.

 

[Delta2]

Take the time derivative of (4) and replace the derivative in the final equation of your last post.

 

[arhzz]

Take the time derivative of (4) and replace the derivative in the final equation of your last post.

Deriving 4;

$$ \frac{di_R(t)}{dt} = \frac{U}{R2+R3}' - \frac{i(t)R_1}{R2+R3}' $$ First one should be 0; the second one

$$ -\frac{R1}{R2+R3} \frac{di(t)}{dt} $$ so 4 derived is;

$$ \frac{di_R(t)}{dt} = -\frac{R1}{R2+R3} \frac{di(t)}{dt} $$

Now plugging that into equation 5

$$ L (\frac{di(t)}{dt} -(-\frac{R1}{R2+R3} \frac{di(t)}{dt}) *\frac{1}{R2+R3} = \frac{ U - i(t)R_1}{R2+R3} $$

Seems like I have 2 derivatives of i(t) now

 

[Delta2]

er yes you have two derivatives but that's not a big problem for algebra, use something like $a\frac{dy}{dt}+b\frac{dy}{dt}=(a+b)\frac{dy}{dt}$.

You can treat the derivative as a normal real number here when you going to apply the distributive property of multiplication with respect to addition, that is $ad+bd=(a+b)d$ where $d=\frac{di}{dt}$.

 

[arhzz]

er yes you have two derivatives but that's not a big problem for algebra, use something like $a\frac{dy}{dt}+b\frac{dy}{dt}=(a+b)\frac{dy}{dt}$.

You can treat the derivative as a normal real number here when you going to apply the distributive property of multiplication with respect to addition, that is $ad+bd=(a+b)d$ where $d=\frac{di}{dt}$.

Ahhh okay, so now it is time for some algebra

$$ \frac{di}{dt} \frac{L}{R2+R3} +\frac{di}{dt} \frac{R_1L}{(R2+R3)^2} = \frac{U-i(t)R1}{R2+R3} $$ I've multipled both sides by R2+R3 and factored out what remains with the derivatives

$$ \frac{di}{dt} (L + \frac{R_1L}{R2+R3}) = U - i(t)R1 $$ Make the bracket to one fraction and move i(t)

$$ \frac{di}{dt} (\frac{L(R2+R3)+R_1L}{R2+R3}) +i(t)R1 = U $$ Now divide with the contents of the bracket should give me;

$$ \frac{di}{dt} + \frac{i(t)R1(R2+R3)}{L(R2+R3) +R_1L} = \frac{U(R2+R3)}{L(R2+R3) +R_1L} $$

By no means the pretties DE but I think its right no? I don't see any further simplifications.

 

[Delta2]

Yes I think its correct.

 

[arhzz]

Yes I think its correct.

Taken me quite a while.Thanks for the help I wouldn't have done it without you.

Cheers!

 

[scottdave]

I recommend you also look at using Laplace transforms to solve this circuit as well.

They can come in handy