In an inertial frame of reference (IFR), there are two fixed points, A and B, which share an entangled state
$$ \frac{1}{\sqrt{2}}(|0>_A|1>_B+|1>_A|0>_B) $$
At point A, a measurement is made. The state then collapses to
$$ |a>_A|b>_B, \{a,b\}=\{0,1\} $$
We assume that A has the state ##|a>_A## and B has ##|b>_B## simultaneously, i.e., when their synchronized clocks both read time T
However, in other inertial frames, due to the relativity of simultaneity, the moment when B has ##|b>_B##...
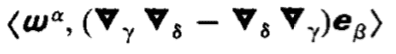 as
as
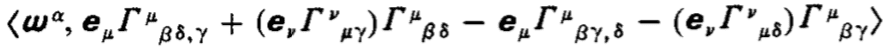 ?
?