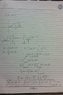Deriving the Area of a Circular Sector Using Integration

  • Context: Undergrad 
  • Thread starter Thread starter Noriele Cruz
  • Start date Start date
  • Tags Tags
    Area Integration
Click For Summary

Discussion Overview

The discussion revolves around the derivation of the area of a circular sector using integration, specifically exploring the formulas A = 1/2 sr and A = 1/2 r²θ. Participants are seeking clarity on the integration process and the application of polar coordinates versus Cartesian coordinates in this context.

Discussion Character

  • Exploratory
  • Technical explanation
  • Debate/contested
  • Mathematical reasoning

Main Points Raised

  • Some participants express confusion about deriving the area of a circular sector using integration and request solutions for the formulas A = 1/2 sr and A = 1/2 r²θ.
  • One participant suggests that using polar coordinates simplifies the derivation, approximating the sector as an isosceles triangle for small angles.
  • Another participant describes dividing the sector into a triangle and a segment for their derivation approach, seeking validation of this method.
  • Some participants discuss their understanding of integrating constants and express uncertainty about simplifying their integration results to the desired formula.
  • A participant mentions a more complicated expression they derived, questioning its relevance to the area of a circular sector.
  • There is a discussion about the nature of the integration process and whether the area can be approximated using triangular formulas as the angle approaches zero.
  • One participant points out that the area of a sector can be expressed in terms of a polar radius function, noting that in the case of a circular sector, the radius is constant.

Areas of Agreement / Disagreement

Participants do not reach a consensus on the best method for deriving the area of a circular sector. Multiple approaches and interpretations are presented, with some participants favoring polar coordinates while others prefer Cartesian methods. The discussion remains unresolved regarding the most effective derivation technique.

Contextual Notes

Participants express varying levels of familiarity with polar coordinates and integration techniques, indicating potential gaps in foundational knowledge that may affect their understanding of the derivation process.

Noriele Cruz
Messages
12
Reaction score
0
I am bothered on how the area of circular sector was derived using integration. I have a solution but I don't know how it will go and come up with the formula:

A = 1/2 sr and A = 1/2 r2 θ

Can someone show me the solution for the derivation of the two formula?
 
Physics news on Phys.org
A basic question, what do you know about an integral?
 
Noriele Cruz said:
I am bothered on how the area of circular sector was derived using integration. I have a solution but I don't know how it will go and come up with the formula:

A = 1/2 sr and A = 1/2 r2 θ

Can someone show me the solution for the derivation of the two formula?
It's an elementary proof if you use polar coordinates.

Examine the small sector in the figure below:

gaussianGraph.gif

​

You can assume for a small angle dθ that the sector is roughly an isosceles triangle, where each side measures r units and the base is r ⋅ dθ units long.

The area of this triangle is dA ≈ (1/2) ⋅ r × r ⋅ dθ = r2 dθ / 2, using the formula for the area of a triangle.

If you want to find the area A of a circular sector between the angles θ1 and θ2, then

$$A = \int_{θ1}^{θ2} \,dA = \int_{θ1}^{θ2} \frac{1}{2} r^2\,dθ = \frac{1}{2} r^2 ⋅ (θ2 - θ1)$$

r ⋅ (θ2 - θ1) is also equivalent to the arc length s, and ##A = \frac{1}{2} r ⋅ s##

Q.E.D.
 
I have done it by means of basic integration of plane areas. I divide the figure into two parts as A1 and A2 for computing the area.
272026.image3.jpg


It is somehow like this (I can't find a picture of my solution). I draw a triangle from A perpendicular to CB. Now, the sector is divided into a triangle and segment. The triangle represents A1 and segment represents A2. Can you show me your solution in my way of derivation?
 
Noriele Cruz said:
I have done it by means of basic integration of plane areas. I divide the figure into two parts as A1 and A2 for computing the area.
272026.image3.jpg


It is somehow like this (I can't find a picture of my solution). I draw a triangle from A perpendicular to CB. Now, the sector is divided into a triangle and segment. The triangle represents A1 and segment represents A2. Can you show me your solution in my way of derivation?
No, because that's a really difficult way to do this problem.

There's nothing wrong with switching to integration using polar coordinates when that method makes the calculation much easier.
 
I am finish in integrating it with values.. I am stuck on how the integration will cancel out to come up with only 1/2 r2 θ for the area.

What do you mean by polar coordinates? I think I work with cartesian coordinates in integrating?
 
Noriele Cruz said:
I am finish in integrating it with values.. I am stuck on how the integration will cancel out to come up with only 1/2 r2 θ for the area.
r is a constant with respect to theta. What happens when you integrate constants?
What do you mean by polar coordinates? I think I work with cartesian coordinates in integrating?
I mean polar coordinates:

https://en.wikipedia.org/wiki/Polar_coordinate_system

If you haven't studied polar coordinates, there is a certain mathematical background which is lacking in your education. You should correct this if you are going to study calculus.
 
I know how to integrate constants. I just don't know how to simplify my solution to 1/2 r2 θ.

We had study about polar coordinates and I know it, I just don't know how to make equations for the integration process.
 
Noriele Cruz said:
I know how to integrate constants. I just don't know how to simplify my solution to 1/2 r2 θ.
You'll have to show your work where you got stuck.
We had study about polar coordinates and I know it, I just don't know how to make equations for the integration process.
I show you how and explained it in Post #3.
 
  • #10
I got this part: πr2 / 4 - r2/2 arcsin (cos θ)

Can you show me how, please?
 
  • #11
This is my solution:
 

Attachments

  • 12788044_1160874747263515_2108366211_n.jpg
    12788044_1160874747263515_2108366211_n.jpg
    32.1 KB · Views: 831
  • #12
Noriele Cruz said:
I got this part: πr2 / 4 - r2/2 arcsin (cos θ)

I'm not even sure what this expression is supposed to represent.

If it's supposed to be the area of a circular sector subtending an angle of 45°, it's way more complicated than it needs to be (and I haven't checked for any mistakes).

https://en.wikipedia.org/wiki/Circular_sector
 
  • #13
Have you checked my solution in the attached file?

For the formula A = 1/2 sr, how it was derived using integration? Sorry for so many questions, I just want to clear up my mind.
 
  • #14
Noriele Cruz said:
Have you checked my solution in the attached file?

I looked at it. It's way too complicated to spend time checking, especially when I have shown you in detail how to obtain a much simpler formula for the area of a circular sector, and showed you documentary proof of the validity of the simple formula.
For the formula A = 1/2 sr, how it was derived using integration? Sorry for so many questions, I just want to clear up my mind.

Again, please refer to Post #3. I showed how this formula is derived from the alternate formula for the area of a circular sector.

If you are not going to read the posts I put up, there's no point in continuing this thread.
 
  • #15
SteamKing said:
It's an elementary proof if you use polar coordinates.

Examine the small sector in the figure below:

gaussianGraph.gif

​

You can assume for a small angle dθ that the sector is roughly an isosceles triangle, where each side measures r units and the base is r ⋅ dθ units long.

The area of this triangle is dA ≈ (1/2) ⋅ r × r ⋅ dθ = r2 dθ / 2, using the formula for the area of a triangle.

If you want to find the area A of a circular sector between the angles θ1 and θ2, then

$$A = \int_{θ1}^{θ2} \,dA = \int_{θ1}^{θ2} \frac{1}{2} r^2\,dθ = \frac{1}{2} r^2 ⋅ (θ2 - θ1)$$

r ⋅ (θ2 - θ1) is also equivalent to the arc length s, and ##A = \frac{1}{2} r ⋅ s##

Q.E.D.

How come my picture of my integration of sector can be drawn like this? Is this also the same with mine?
 
  • #16
Noriele Cruz said:
How come my picture of my integration of sector can be drawn like this? Is this also the same with mine?
All circular sectors look alike.

The dA in the figure is actually drawn for the case where r is not a constant but instead varies with the angle θ.

For a circular sector, r is constant, and integrating r and θ is not necessary to find the area of the sector.
 
  • #17
How about the curve in the part of the sector? If I'm not mistaken, the figure you posted is somehow a triangle rather than a sector with curve part.
Where is it?
 
  • #18
Noriele Cruz said:
How about the curve in the part of the sector? If I'm not mistaken, the figure you posted is somehow a triangle rather than a sector with curve part.
Where is it?
In the limit, as dθ → 0, then the arc portion of the sector is naturally going to appear more and more like a straight line segment, which is why the area of this tiny sector can be approximated using the formula for the area of a triangle.

To find the area of circular sector ABC, as shown in Post #4, that sector would be subdivided into many little slivers each sweeping out an angle dθ. The integration process adds up the areas dA of these segments as dθ → 0, producing a finite value A for the area of sector ABC.
 
  • #19
In general, the area of a sector bounded by a curve ##C## defined by polar radius ##\rho(\theta)##, such that ##C = \rho([\theta_1,\theta_2])## , is ## A= \frac{1}{2} \int_{\theta_1}^{\theta_2} \rho^2(\theta) \ d\theta ## . In your case, ##\rho(\theta)## is constant and equal to ##r## since your sector is circular.
 

Similar threads

MHB What is the maximum area of the circular sector with a perimeter of 12 cm?
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad The net area and total area involving definite integrals
  • · Replies 2 ·
Replies
2
Views
2K
Undergrad Negative area above x-axis from integrating x^2?
  • · Replies 4 ·
Replies
4
Views
3K
Undergrad Double integrals - do areas cancel?
  • · Replies 24 ·
Replies
24
Views
4K
Undergrad What's my mistake in this integration problem?
  • · Replies 8 ·
Replies
8
Views
3K
Undergrad Does this "theorem" of limits hold in general?
  • · Replies 1 ·
Replies
1
Views
1K
Undergrad Definite integral is undefined and not undefined
  • · Replies 8 ·
Replies
8
Views
3K
Undergrad Question about Integrals to Determine Volume vs Surface Area
  • · Replies 5 ·
Replies
5
Views
3K
Undergrad Formula for integration of natural coordinates over an element
  • · Replies 3 ·
Replies
3
Views
2K
High School Calculating shaded area: I'm getting discrepancies between methods
  • · Replies 3 ·
Replies
3
Views
3K