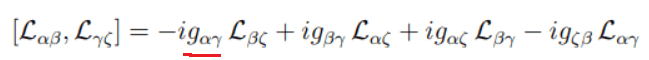Deriving the commutation relations of the Lie algebra of Lorentz group

[bella987]

Homework Statement

Find commutation relations for Lorentz group

Relevant Equations

See below.

This is the defining generator of the Lorentz group

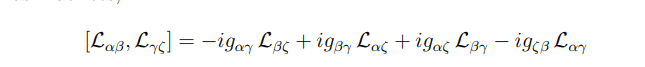
which is then divided into subgroups for rotations and boosts

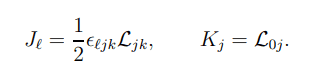
And I then want to find the commutation relation [J_m, J_n] (and [J_m, K_n] ). I'm following this derivation, but am having a hard time to understand all the steps:

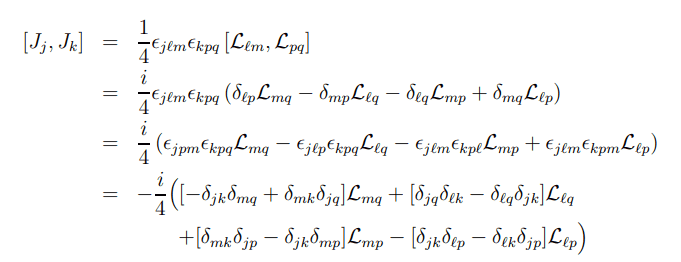
especially between here and the following step

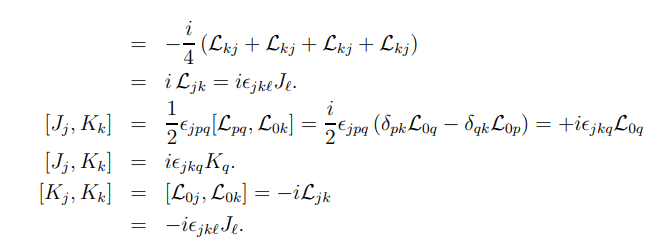
Could someone explain to someone just getting familiar with the Levi-Cevita symbol and its Kronecker delta dependence, what exactly is going on from step to step here? I would be so grateful!!

 

[malawi_glenn]

Indices with roman letters are spatial right, and greek time + spatial?
What definition of minkowski metric you have? Diag(+,-,-,-) or Diag(-,+,+,+)?

 

[bella987]

Hmm, the greek letters are definitely time + spatial, but in the second included equation we divide the 6 generators into three spatial ones (rotations) and three temporal ones (boosts), so the roman ones are used when seperating them like that.
And it's mostly minus metric.

 

[malawi_glenn]

Ok, great.
Well that is the first step. $g_{\alpha \gamma}$ becomes $- \delta_{ac}$.

Do you know anything about the $\mathcal{L}$ i.e. are they symmetric or anti-symmetric? This will help you simplify identities with kroneckers and levi-civitas.

Use

and calculate the commutator

show first that this equals

just by replacing $g$ with kroeckers and using the defining commutation amongs $\mathcal{L}$.

As per the forum rules, you must show your attempt at a solution. "I do not understand" is not enough.