Describing motion of a particle qualitatively

[ChiralSuperfields]

Homework Statement

See below

Relevant Equations

Position vector is the same as integral of velocity vector

For part (a) and (b) of this problem,

The solution is,

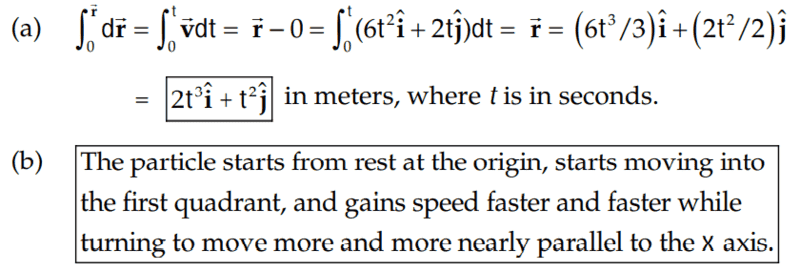
However, how did they arrive at their conclusion in part(b)?

As you can't graph it on a GC, I decide to imagine plugging in values for t, which I see that the 2t^3 grows quicker than the t^2 which is why I think they said that the particle will asymptote with the x-axis.

Anybody else have a different way at arriving at the conclusion given in part(b)? Feel free to let me know!

Many thanks!

 

[malawi_glenn]

can you calculate the velocity vector at t=0?

Define the angle that the particle moves in the x-y plane as $\theta$ you have $\tan \theta = \dfrac{v_y}{v_x}$. Now what is the limit of this angle as $t \to \infty$?

 

[ChiralSuperfields]

Thanks!

 

[malawi_glenn]

View attachment 318155 Thanks!

that is not correct.

 

[vela]

As you can't graph it on a GC, I decide to imagine plugging in values for t, which I see that the 2t^3 grows quicker than the t^2 which is why I think they said that the particle will asymptote with the x-axis.

You have the right idea, but it's not correct to say it "will asymptote with the x-axis" as that implies $y \to 0$ as $x \to \infty$. In fact, there is no asymptote since both $x$ and $y$ grow without bound as $t \to \infty$.

 

[ChiralSuperfields]

Thanks for your replies @malawi_glenn and @vela! Sorry I think I evaluated the limit incorrectly, is this correct now?

Since this is the angle between the horizontal and the velocity vector of the particle after an infinite time, could someone please explain to me how the particle dose not asymptote with the x-axis if my equation is correct? I thought that the x-component of the velocity would increase faster than the y-component of the velocity since it is squared.

Many thanks!

 

[malawi_glenn]

could someone please explain to me how the particle dose not asymptote with the x-axis if my equation is correct?

See velas reply.

(x(t), y(t)) = (2t^3 , t^2)

Can you draw this curve in the x-y plane?

 

[ChiralSuperfields]

See velas reply.

(x(t), y(t)) = (2t^3 , t^2)

Can you draw this curve in the x-y plane?

Yes, you just in terms of the third variable t?

 

[malawi_glenn]

Yes, you just in terms of the third variable t?

Hint: solve t in terms of x first, then find y in terms of x.

 

[ChiralSuperfields]

Hint: solve t in terms of x first, then find y in terms of x.

Thanks for your reply @malawi_glenn ,

,

I put it into Desmos I can see that I dose not really asymptote with the x-axis. https://www.desmos.com/calculator/habtdbe3mt

However, what was wrong with the way I found the angle previously?

Many thanks!

 

[malawi_glenn]

However, what was wrong with the way I found the angle previously?

You posted one attempt first, I said it was wrong. Then you gave the correct one.

 

[Orodruin]

That the angle goes to zero does not mean that the x-axis becomes an asymptote. The simplest counter example would be the constant function y(x) = k with k different from 0. This clearly has y = k as the asymptote but the angle approaches 0 as x goes to infinity.

 

[vela]

Since this is the angle between the horizontal and the velocity vector of the particle after an infinite time, could someone please explain to me how the particle dose not asymptote with the x-axis if my equation is correct?

First, asymptote is a noun, not a verb. :) I think you mean the curve gets closer and closer to becoming parallel to the x-axis, which you showed by evaluating the limit, not that it's asymptotic to the x-axis.

Second, for the x-axis to be an asymptote, the particle's trajectory would have to get arbitrarily close the the x-axis without crossing it as $x \to \infty$. Your results, however, shows that the particle gets farther from the x-axis as it moves.

It may seem counterintuitive that the curve can approach becoming horizontal yet still remain unbounded. It's one of the things you have to be careful about when dealing with infinity.

 

[Orodruin]

Second, for the x-axis to be an asymptote, the particle's trajectory would have to get arbitrarily close the the x-axis without crossing it as x→∞.

My emphasis.

There is nothing stopping a function from crossing its asymptote. Consider $\sin(x)/x$ which has the $x$ axis as an asymptote yet crosses it an infinite number of times.

 

[PeroK]

It may seem counterintuitive that the curve can approach becoming horizontal yet still remain unbounded.

A good example is the function $y = \ln x$ where $\dfrac{dy}{dx} = \dfrac 1 x$.

 

[ChiralSuperfields]

So I was correct to find the angle goes to zero for the angle the finial velocity vector makes with the horizontal? However, my interpretation of what that angle meant was wrong? What if I found the angle that the finial position vector makes with the horizontal?

Many thanks!

 

[kuruman]

Here is a parametric plot that says it all. Consider a point on the solid line to represent the position of the particle as it moves in the xy-plane. Describe the motion.

 

[ChiralSuperfields]

Here is a parametric plot that says it all. Consider a point on the solid line to represent the position of the particle as it moves in the xy-plane. Describe the motion.

View attachment 318214

Thanks for your reply @kuruman ! The motion of the particle looks to me like half of a horizontal parabola. At small time values there is a rapid increase in y-values however, after larger time values the y and x position increase at the same rate. It looks like after large time values the parametric can be extrapolated as a straight line that makes an angle of 45 degrees with the horizontal.

Are you trying to say that I calculated the angle of the velocity vector after an infinite time interval incorrectly (post #6)?

Many thanks!

 

[kuruman]

Are you trying to say that I calculated the angle of the velocity vector after an infinite time interval incorrectly (post #6)?

Yes, I am. Just look at the velocity vector, $\mathbf{v}=6t^2~\mathbf{\hat i}+2t~\mathbf{\hat j}.$ In order for the particle to move parallel to the x-axis, the y-component of the velocity must decrease and approach zero as time increases. Actually, the y-component increases linearly with increasing time, so it will never go to zero. Of course, the x-component increases faster than the y-component which means, as the solution says, that the particle will turn to move closer to being parallel to the x-axis. However, it will never be parallel to the x-axis, even after infinite time has elapsed.

 

[ChiralSuperfields]

Yes, I am. Just look at the velocity vector, $\mathbf{v}=6t^2~\mathbf{\hat i}+2t~\mathbf{\hat j}.$ In order for the particle to move parallel to the x-axis, the y-component of the velocity must decrease and approach zero as time increases. Actually, the y-component increases linearly with increasing time, so it will never go to zero. Of course, the x-component increases faster than the y-component which means, as the solution says, that the particle will turn to move closer to being parallel to the x-axis. However, it will never be parallel to the x-axis, even after infinite time has elapsed.

Thanks for your reply @kuruman! How do you calculate the angle correctly (is it 45 degrees)? I should be able to find it using the velocity vector or position vector method?

Many thanks!

 

[kuruman]

If you are asking about the angle $\theta$ of the velocity vector relative to the x-axis, $\tan\theta=\dfrac{v_y}{v_x}=\dfrac{1}{3t}.$ It is equal to 45° at $t=\frac{1}{3}$ time units.

 

[ChiralSuperfields]

If you are asking about the angle $\theta$ of the velocity vector relative to the x-axis, $\tan\theta=\dfrac{v_y}{v_x}=\dfrac{1}{3t}.$ It is equal to 45° at $t=\frac{1}{3}$ time units.

Sorry @kuruman, I was asking what the velocity vector would be at t = infinity time units.

Many thanks!

 

[kuruman]

Sorry @kuruman, I was asking what the velocity vector would be at t = infinity time units.

Many thanks!

You know that $\mathbf{v}=6t^2~\mathbf{\hat i}+2t~\mathbf{\hat j}.$ Put in $t=\infty$ and see what you get.

 

[ChiralSuperfields]

You know that $\mathbf{v}=6t^2~\mathbf{\hat i}+2t~\mathbf{\hat j}.$ Put in $t=\infty$ and see what you get.

Sorry @kuruman, I think I have confused myself. I am not asking what the velocity vector is at time at t = infinity, but the angle the velocity vector makes with the horizontal at t = infinity.

Is this correct?

Manyh thanks!

 

[kuruman]

The fact remains that as long as the velocity has a non-zero y-component, the angle will never be zero but will have some finite value. You can argue that $$\lim_{t \rightarrow \infty} \left({\frac {1} {3t}}\right)=0$$all you want, but you cannot argue that the "$1$" in the numerator of the fraction is zero. It doesn't happen, not even for small values of $1$.

 

[ChiralSuperfields]

The fact remains that as long as the velocity has a non-zero y-component, the angle will never be zero but will have some finite value. You can argue that $$\lim_{t \rightarrow \infty} \left({\frac {1} {3t}}\right)=0$$all you want, but you cannot argue that the "$1$" in the numerator of the fraction is zero. It doesn't happen, not even for small values of $1$.

Thanks for your reply @kuruman!

So we are not really looking for the behavior of the position function for very larger values of time. So when they said 'describe the motion quantitively' they were really talking about for some values of t, in which case the angle that the position vector at some later time t is non-zero.

Many thanks!

 

[kuruman]

Thanks for your reply @kuruman!

So we are not really looking for the behavior of the position function for very larger values of time. So when they said 'describe the motion quantitively' they were really talking about for some values of t, in which case the angle that the position vector at some later time t is non-zero.

Many thanks!

Yes. The boxed answer in the solution for part (b) is what I would have written. I repeat, the angle is always non-zero for reasons I have already explained. Also, the statement of the problem says "describe the motion qualitatively" (emphasis mine), not quantitively.

 

[ChiralSuperfields]

Yes. The boxed answer in the solution for part (b) is what I would have written. I repeat, the angle is always non-zero for reasons I have already explained. Also, the statement of the problem says "describe the motion qualitatively" (emphasis mine), not quantitively.

Ok thanks @kuruman ! I will also see what happens when I find the angle the position vector makes with the horizontal for various time values.

Many thanks!

 

[ChiralSuperfields]

Ok thanks @kuruman ! I will also see what happens when I find the angle the position vector makes with the horizontal for various time values.

Many thanks!

Ok thank you very much @kuruman !