- #1
Prometheus18
- 3
- 1
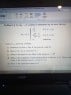
Hello. I'm using Griffiths' introductory textbook on quantum mechanics, which I have just begun, and have arrived at a question on a simple wave function:

The answer to the first question I know to be √(3/b).
The answer to part e is (2a + b) / 4.
My problem is that I don't understand how there is any difference between the most likely position of the particle on the X axis and its expected value, given above for part e.
I have checked the solution manual and its its answer to part c was just 'a', which was my initial instinct, because the graph reaches its maximum at a. But this seems to me to be contrary to the notion of an expected value which, among other things, in a probability context should be the most likely value.
Has the solutions manual got it wrong, or have I?
The answer to the first question I know to be √(3/b).
The answer to part e is (2a + b) / 4.
My problem is that I don't understand how there is any difference between the most likely position of the particle on the X axis and its expected value, given above for part e.
I have checked the solution manual and its its answer to part c was just 'a', which was my initial instinct, because the graph reaches its maximum at a. But this seems to me to be contrary to the notion of an expected value which, among other things, in a probability context should be the most likely value.
Has the solutions manual got it wrong, or have I?