SUMMARY
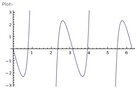
The discussion focuses on determining the exact solutions to the trigonometric equation using a TI-83+ graphing calculator. The user inputs the function as y = 6(1/cos(X))^2*tan(X) - 12tan(X) and seeks to find solutions within the interval [0, 360) degrees. Despite initially observing 7 roots on the graph, the user confirms there are 6 valid solutions after considering the domain restrictions, specifically excluding the root at x = 2π. The conversation emphasizes the importance of correctly interpreting the graph and the domain when counting solutions.
PREREQUISITES
- Understanding of trigonometric functions and their properties
- Familiarity with graphing calculators, specifically the TI-83+
- Knowledge of radians and degrees conversion
- Basic concepts of function roots and domain restrictions
NEXT STEPS
- Learn how to graph trigonometric functions on the TI-83+ calculator
- Study the relationship between radians and degrees in trigonometry
- Explore methods for identifying roots of functions graphically
- Investigate domain restrictions and their impact on function solutions
USEFUL FOR
Students, educators, and anyone involved in learning or teaching trigonometry, particularly those using graphing calculators to solve equations.