Determine the final train speed (mass and slinky on a train)

[leafy]

Homework Statement

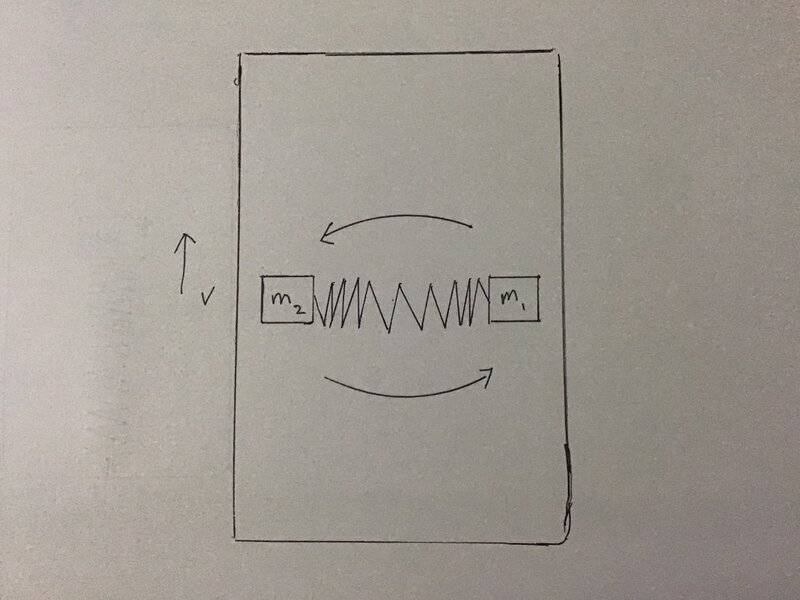
Top view of the train shown a rotating pair of mass m1 and m2 attached to a slinky. The train is moving north with constant speed v. At 0 degree, m1 is released from the slinky and move north to hit the train inelasticly. The slinky is fully contract when the system rotate 180 degrees. During this time, m2 continue to go in circle until 180 degrees. m2 is then released from the slinky and move north to hit the train. Determine the final speed of the train:

A) speed up
B) slow down
C) remain the same

Relevant Equations

F = dv/dt

A, the train speed up?

 

[haruspex]

What is your reasoning?

 

[leafy]

We have two masses hitting the train north, so the speed increase. However, after rethinking about the slinky mass (since mass is require for a force) has momentum component heading south. The overall speed of the train remain the same. But the interesting thing I'm thinking is can we actually delay the momentum.

 

[haruspex]

We have two masses hitting the train north, so the speed increase. However, after rethinking about the slinky mass (since mass is require for a force) has momentum component heading south. The overall speed of the train remain the same. But the interesting thing I'm thinking is can we actually delay the momentum.

Not entirely sure what you meant by some of that. Does "slinky mass" refer to the mass of the slinky itself? And what do you mean by "delaying" momentum?

Think about how the second mass gets to be going N after initially going S.

 

[leafy]

yes, slinky are masses and springs connected in series. What I meant by delay momentum is slinky action redistribute the center of mass without an external force. If you see a slinky drop from a rooftop, the top part fall down faster, which means the center of mass change as it drop.

After the first mass is relase, the forces still acting on the second mass until the slinky is full contracted. That's how the second mass go north. Just like when the sun disappear, the Earth still going in circle until gravity catch on.

 

[haruspex]

After the first mass is relase, the forces still acting on the second mass

And what is providing that force?

 

[LCSphysicist]

yes, slinky are masses and springs connected in series. What I meant by delay momentum is slinky action redistribute the center of mass without an external force. If you see a slinky drop from a rooftop, the top part fall down faster, which means the center of mass change as it drop.

After the first mass is relase, the forces still acting on the second mass until the slinky is full contracted. That's how the second mass go north. Just like when the sun disappear, the Earth still going in circle until gravity catch on.

The Earth still go on ellipse because information can't move faster than light. I am almost sure the problem here don't want you to invoke relativity, but just classical mechanics.

Apart from the fact that, even if it want you to invoke relativity, you would still be wrong

 

[leafy]

And what is providing that force?

the stretched slinky, when unstretched, provides the force.

The Earth still go on ellipse because information can't move faster than light. I am almost sure the problem here don't want you to invoke relativity, but just classical mechanics.

Apart from the fact that, even if it want you to invoke relativity, you would still be wrong

It's resembled. The second mass still move in circle even when the first mass disconnected because pressure wave need time to reach the second mass.

 

[haruspex]

the stretched slinky

And what holds that in place?

 

[haruspex]

like when the sun disappear, the Earth still going in circle until gravity catch on.

I have no idea what you are talking about. Gravity acts all the time, whether you can see the sun or not.

 

[leafy]

And what holds that in place?

initially the two mass stretched the slinky, after m1 release, the slinky contract toward the second mass.

I have no idea what you are talking about. Gravity acts all the time, whether you can see the sun or not.

nevermind

 

[haruspex]

initially the two mass stretched the slinky, after m1 release, the slinky contract toward the second mass.

That doesn’t answer my question.
Why doesn’t the slinky hit the S end of the train?

 

[leafy]

That doesn’t answer my question.
Why doesn’t the slinky hit the S end of the train?

It should. That's why I say there is no speed change in the train.

 

[haruspex]

It should. That's why I say there is no speed change in the train.

Yet, we are told the second mass hits the front. I can only see twomways that can happen:
1. The slinky is fixed to an axis at its middle.
2. The slinky is massive, and the second mass is released after a 270° turn, or nearly, so projected N by the expanding slinky.

I don't really understand the text regarding the contraction of the slinky. Is it by some magic staying contracted during the 180° turn?

Where does this question come from?