SUMMARY
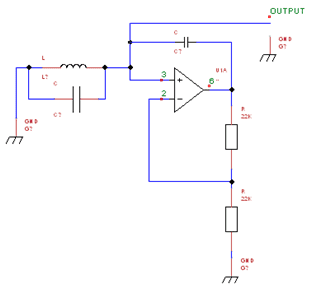
This discussion focuses on determining the frequency of an oscillator circuit affected by a feedback capacitor. The circuit utilizes an op-amp configured as a low-pass filter, specifically an integrator, which influences the oscillation frequency. Key values mentioned include a tank circuit capacitor of 10 µF, a feedback capacitor of 470 µF, and an oscillation frequency of 2174 Hz. The conversation highlights the importance of understanding the negative impedance introduced by the feedback capacitor and its role in maintaining oscillations within the circuit.
PREREQUISITES
- Understanding of op-amp configurations, particularly integrators
- Knowledge of LC tank circuits and their resonant frequency calculations
- Familiarity with negative impedance concepts
- Basic principles of feedback in electronic circuits
NEXT STEPS
- Research the effects of feedback capacitors on oscillator stability
- Learn about negative impedance converters and their applications
- Study the principles of op-amp low-pass filters and their frequency response
- Investigate the impact of equivalent series resistance (ESR) in capacitors on circuit performance
USEFUL FOR
Electronics engineers, circuit designers, and hobbyists interested in oscillator design and feedback systems will benefit from this discussion.